Collecting and Analyzing Multidimensional Data with Local Differential Privacy
Paper and Code
Jun 28, 2019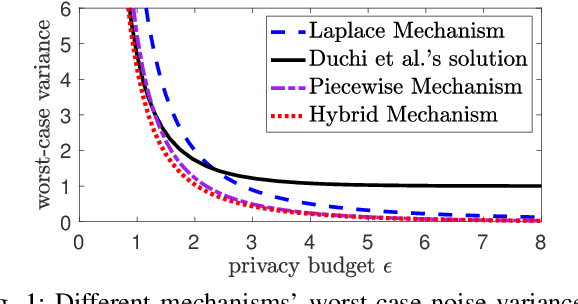
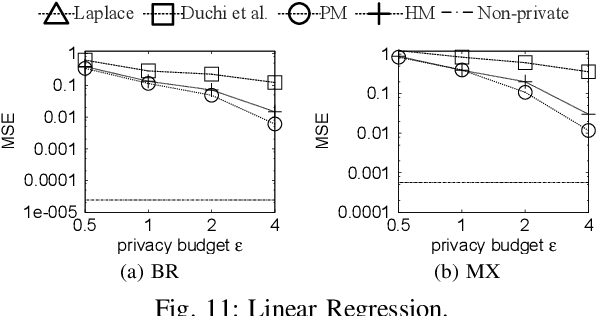
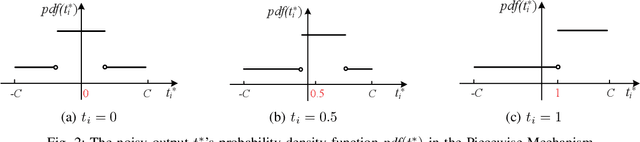
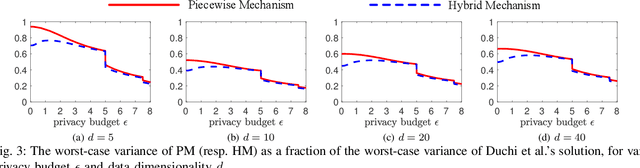
Local differential privacy (LDP) is a recently proposed privacy standard for collecting and analyzing data, which has been used, e.g., in the Chrome browser, iOS and macOS. In LDP, each user perturbs her information locally, and only sends the randomized version to an aggregator who performs analyses, which protects both the users and the aggregator against private information leaks. Although LDP has attracted much research attention in recent years, the majority of existing work focuses on applying LDP to complex data and/or analysis tasks. In this paper, we point out that the fundamental problem of collecting multidimensional data under LDP has not been addressed sufficiently, and there remains much room for improvement even for basic tasks such as computing the mean value over a single numeric attribute under LDP. Motivated by this, we first propose novel LDP mechanisms for collecting a numeric attribute, whose accuracy is at least no worse (and usually better) than existing solutions in terms of worst-case noise variance. Then, we extend these mechanisms to multidimensional data that can contain both numeric and categorical attributes, where our mechanisms always outperform existing solutions regarding worst-case noise variance. As a case study, we apply our solutions to build an LDP-compliant stochastic gradient descent algorithm (SGD), which powers many important machine learning tasks. Experiments using real datasets confirm the effectiveness of our methods, and their advantages over existing solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge