Boosting offline handwritten text recognition in historical documents with few labeled lines

In this paper, we face the problem of offline handwritten text recognition (HTR) in historical documents when few labeled samples are available and some of them contain errors in the train set. Three main contributions are developed. First we analyze how to perform transfer learning (TL) from a massive database to a smaller historical database, analyzing which layers of the model need a fine-tuning process. Second, we analyze methods to efficiently combine TL and data augmentation (DA). Finally, an algorithm to mitigate the effects of incorrect labelings in the training set is proposed. The methods are analyzed over the ICFHR 2018 competition database, Washington and Parzival. Combining all these techniques, we demonstrate a remarkable reduction of CER (up to 6% in some cases) in the test set with little complexity overhead.

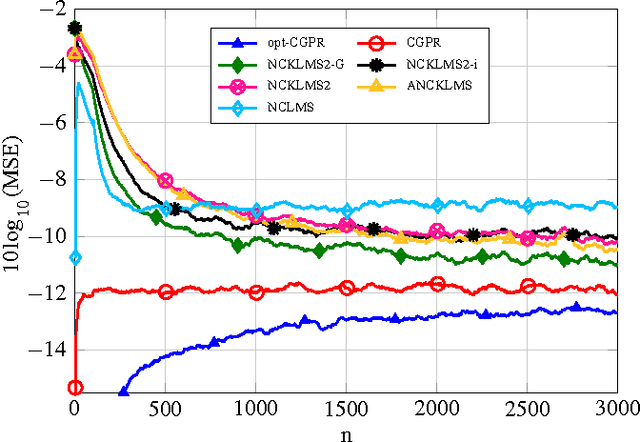
The Generalized Complex Kernel Least-Mean-Square Algorithm

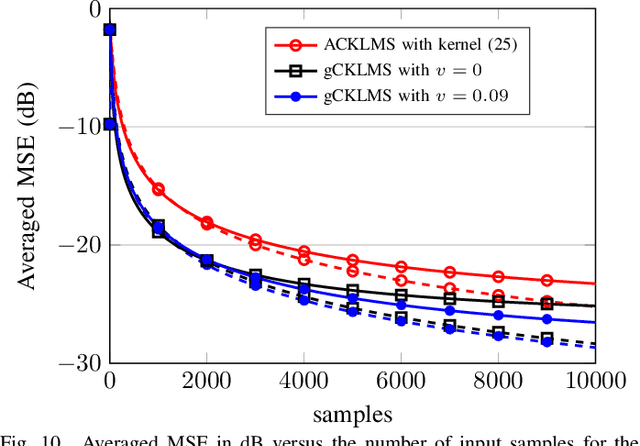
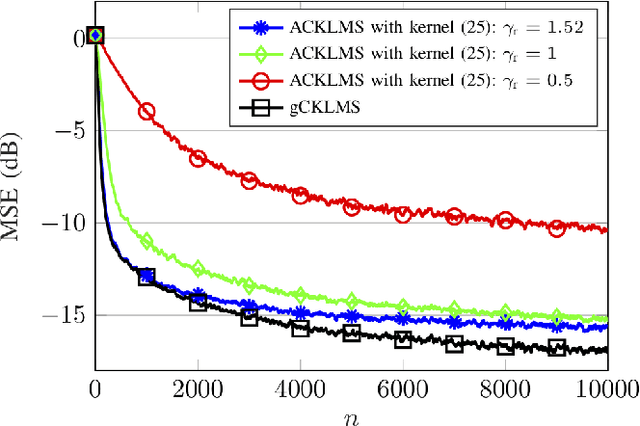
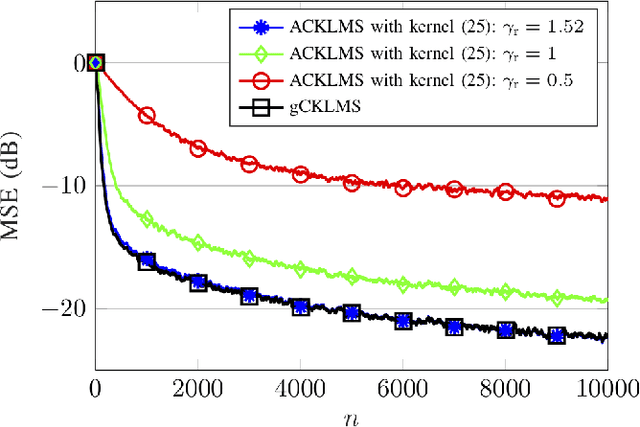
We propose a novel adaptive kernel based regression method for complex-valued signals: the generalized complex-valued kernel least-mean-square (gCKLMS). We borrow from the new results on widely linear reproducing kernel Hilbert space (WL-RKHS) for nonlinear regression and complex-valued signals, recently proposed by the authors. This paper shows that in the adaptive version of the kernel regression for complex-valued signals we need to include another kernel term, the so-called pseudo-kernel. This new solution is endowed with better representation capabilities in complex-valued fields, since it can efficiently decouple the learning of the real and the imaginary part. Also, we review previous realizations of the complex KLMS algorithm and its augmented version to prove that they can be rewritten as particular cases of the gCKLMS. Furthermore, important conclusions on the kernels design are drawn that help to greatly improve the convergence of the algorithms. In the experiments, we revisit the nonlinear channel equalization problem to highlight the better convergence of the gCKLMS compared to previous solutions. Also, the flexibility of the proposed generalized approach is tested in a second experiment with non-independent real and imaginary parts. The results illustrate the significant performance improvements of the gCKLMS approach when the complex-valued signals have different properties for the real and imaginary parts.

Inference in Deep Gaussian Processes using Stochastic Gradient Hamiltonian Monte Carlo

Deep Gaussian Processes (DGPs) are hierarchical generalizations of Gaussian Processes that combine well calibrated uncertainty estimates with the high flexibility of multilayer models. One of the biggest challenges with these models is that exact inference is intractable. The current state-of-the-art inference method, Variational Inference (VI), employs a Gaussian approximation to the posterior distribution. This can be a potentially poor unimodal approximation of the generally multimodal posterior. In this work, we provide evidence for the non-Gaussian nature of the posterior and we apply the Stochastic Gradient Hamiltonian Monte Carlo method to directly sample from it. To efficiently optimize the hyperparameters, we introduce the Moving Window MCEM algorithm. This results in significantly better predictions at a lower computational cost than its VI counterpart. Thus our method establishes a new state-of-the-art for inference in DGPs.

Boosting Handwriting Text Recognition in Small Databases with Transfer Learning

In this paper we deal with the offline handwriting text recognition (HTR) problem with reduced training datasets. Recent HTR solutions based on artificial neural networks exhibit remarkable solutions in referenced databases. These deep learning neural networks are composed of both convolutional (CNN) and long short-term memory recurrent units (LSTM). In addition, connectionist temporal classification (CTC) is the key to avoid segmentation at character level, greatly facilitating the labeling task. One of the main drawbacks of the CNNLSTM-CTC (CLC) solutions is that they need a considerable part of the text to be transcribed for every type of calligraphy, typically in the order of a few thousands of lines. Furthermore, in some scenarios the text to transcribe is not that long, e.g. in the Washington database. The CLC typically overfits for this reduced number of training samples. Our proposal is based on the transfer learning (TL) from the parameters learned with a bigger database. We first investigate, for a reduced and fixed number of training samples, 350 lines, how the learning from a large database, the IAM, can be transferred to the learning of the CLC of a reduced database, Washington. We focus on which layers of the network could be not re-trained. We conclude that the best solution is to re-train the whole CLC parameters initialized to the values obtained after the training of the CLC from the larger database. We also investigate results when the training size is further reduced. The differences in the CER are more remarkable when training with just 350 lines, a CER of 3.3% is achieved with TL while we have a CER of 18.2% when training from scratch. As a byproduct, the learning times are quite reduced. Similar good results are obtained from the Parzival database when trained with this reduced number of lines and this new approach.

Deep Gaussian Processes with Decoupled Inducing Inputs

Deep Gaussian Processes (DGP) are hierarchical generalizations of Gaussian Processes (GP) that have proven to work effectively on a multiple supervised regression tasks. They combine the well calibrated uncertainty estimates of GPs with the great flexibility of multilayer models. In DGPs, given the inputs, the outputs of the layers are Gaussian distributions parameterized by their means and covariances. These layers are realized as Sparse GPs where the training data is approximated using a small set of pseudo points. In this work, we show that the computational cost of DGPs can be reduced with no loss in performance by using a separate, smaller set of pseudo points when calculating the layerwise variance while using a larger set of pseudo points when calculating the layerwise mean. This enabled us to train larger models that have lower cost and better predictive performance.

Complex-Valued Kernel Methods for Regression

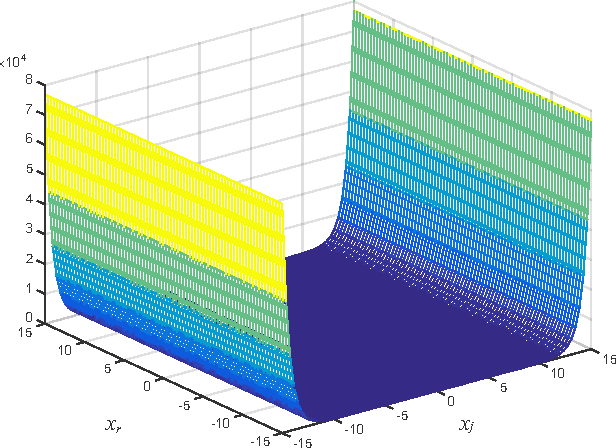
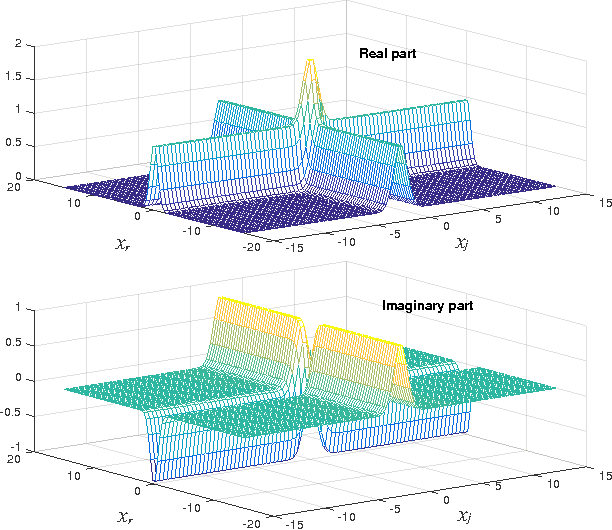
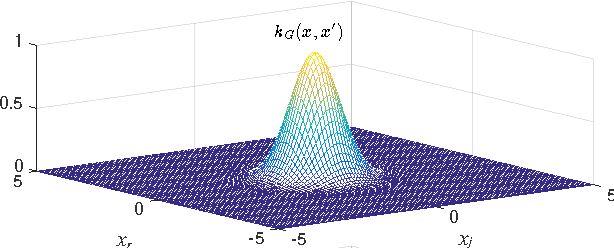
Usually, complex-valued RKHS are presented as an straightforward application of the real-valued case. In this paper we prove that this procedure yields a limited solution for regression. We show that another kernel, here denoted as pseudo kernel, is needed to learn any function in complex-valued fields. Accordingly, we derive a novel RKHS to include it, the widely RKHS (WRKHS). When the pseudo-kernel cancels, WRKHS reduces to complex-valued RKHS of previous approaches. We address the kernel and pseudo-kernel design, paying attention to the kernel and the pseudo-kernel being complex-valued. In the experiments included we report remarkable improvements in simple scenarios where real a imaginary parts have different similitude relations for given inputs or cases where real and imaginary parts are correlated. In the context of these novel results we revisit the problem of non-linear channel equalization, to show that the WRKHS helps to design more efficient solutions.

Proper Complex Gaussian Processes for Regression

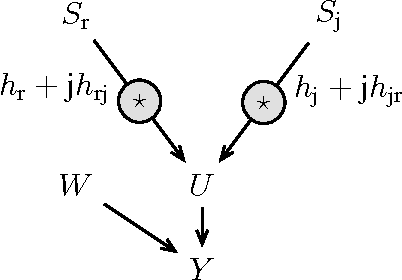
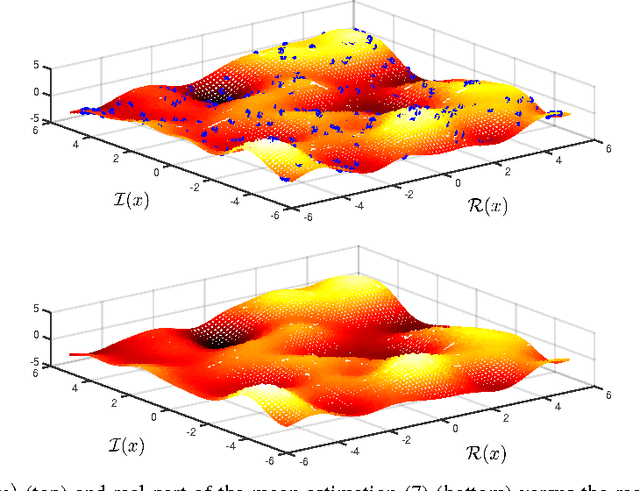
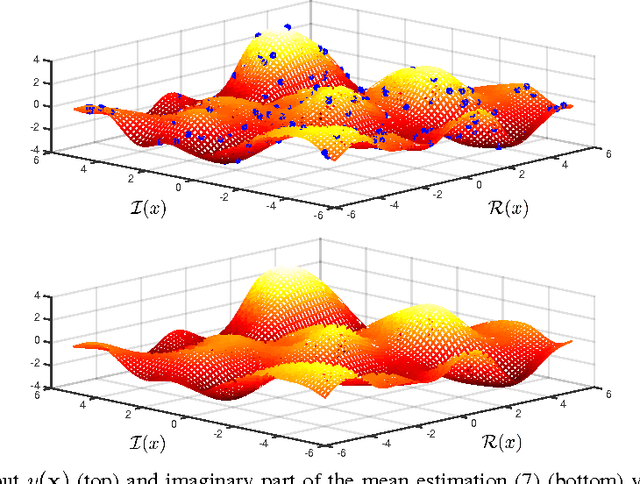
Complex-valued signals are used in the modeling of many systems in engineering and science, hence being of fundamental interest. Often, random complex-valued signals are considered to be proper. A proper complex random variable or process is uncorrelated with its complex conjugate. This assumption is a good model of the underlying physics in many problems, and simplifies the computations. While linear processing and neural networks have been widely studied for these signals, the development of complex-valued nonlinear kernel approaches remains an open problem. In this paper we propose Gaussian processes for regression as a framework to develop 1) a solution for proper complex-valued kernel regression and 2) the design of the reproducing kernel for complex-valued inputs, using the convolutional approach for cross-covariances. In this design we pay attention to preserve, in the complex domain, the measure of similarity between near inputs. The hyperparameters of the kernel are learned maximizing the marginal likelihood using Wirtinger derivatives. Besides, the approach is connected to the multiple output learning scenario. In the experiments included, we first solve a proper complex Gaussian process where the cross-covariance does not cancel, a challenging scenario when dealing with proper complex signals. Then we successfully use these novel results to solve some problems previously proposed in the literature as benchmarks, reporting a remarkable improvement in the estimation error.

Gaussian Processes for Nonlinear Signal Processing

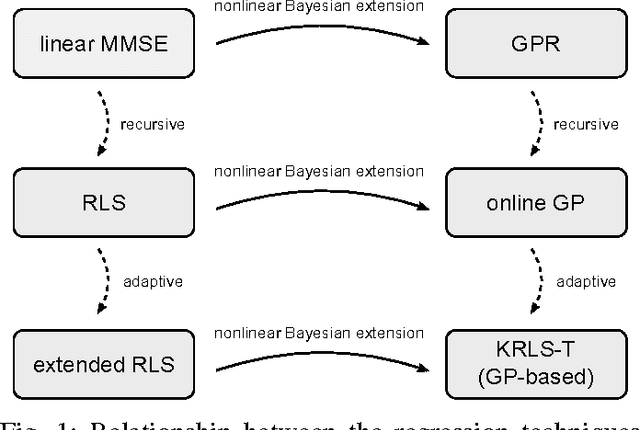
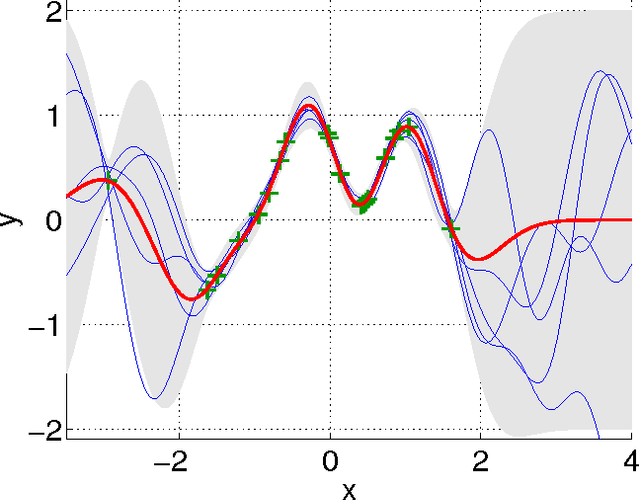
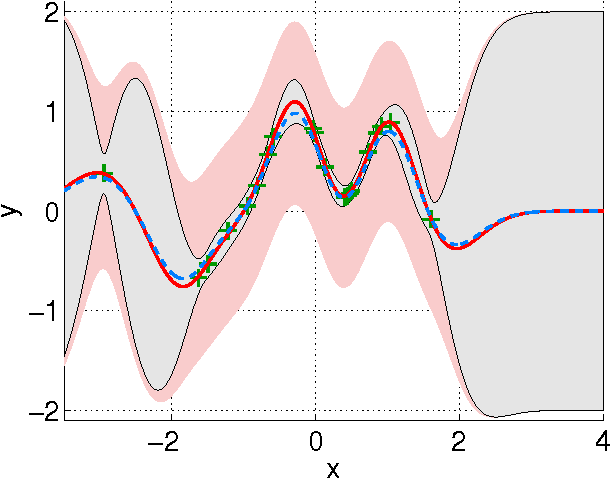
Gaussian processes (GPs) are versatile tools that have been successfully employed to solve nonlinear estimation problems in machine learning, but that are rarely used in signal processing. In this tutorial, we present GPs for regression as a natural nonlinear extension to optimal Wiener filtering. After establishing their basic formulation, we discuss several important aspects and extensions, including recursive and adaptive algorithms for dealing with non-stationarity, low-complexity solutions, non-Gaussian noise models and classification scenarios. Furthermore, we provide a selection of relevant applications to wireless digital communications.