Complex-Valued Gaussian Processes for Regression

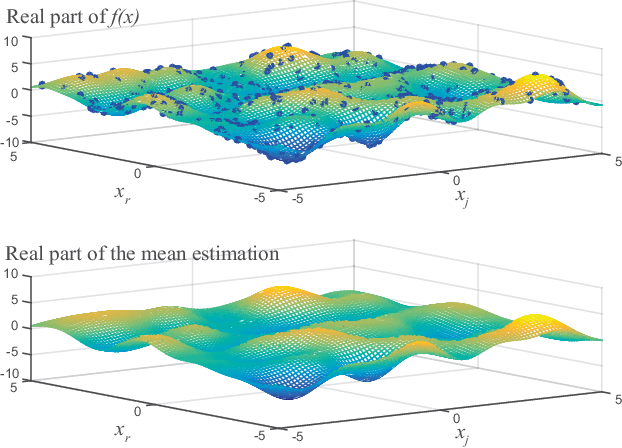
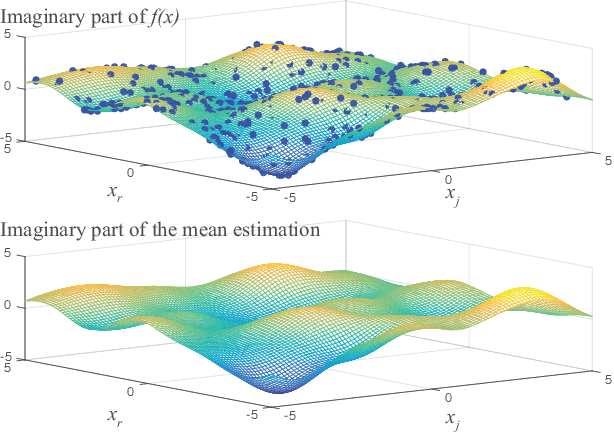
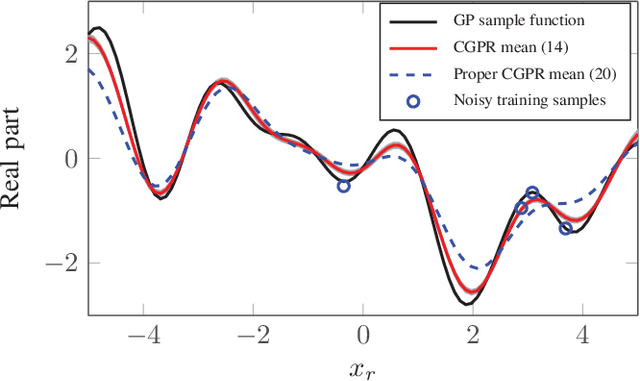
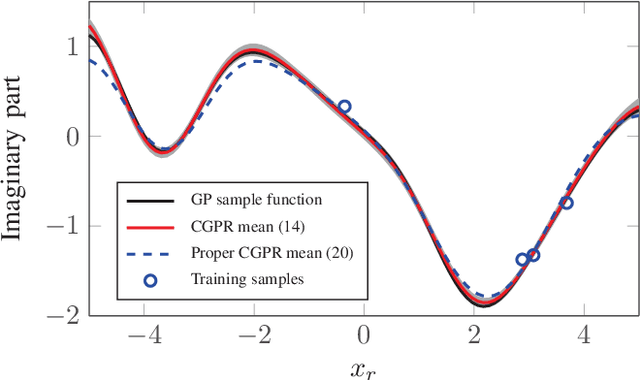
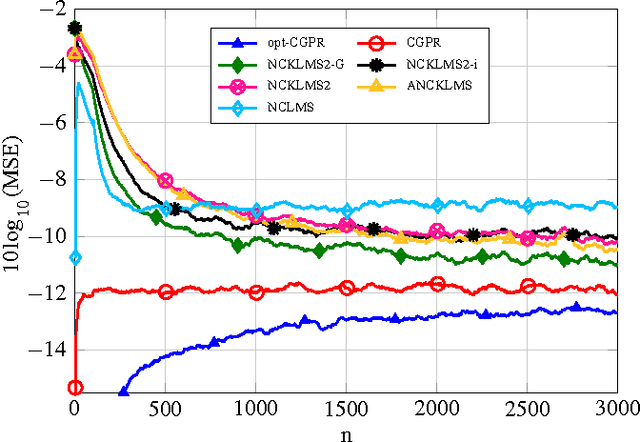
In this paper we propose a novel Bayesian solution for nonlinear regression in complex fields. Previous solutions for kernels methods usually assume a complexification approach, where the real-valued kernel is replaced by a complex-valued one. This approach is limited. Based on results in complex-valued linear theory and Gaussian random processes we show that a pseudo-kernel must be included. This is the starting point to develop the new complex-valued formulation for Gaussian process for regression (CGPR). We face the design of the covariance and pseudo-covariance based on a convolution approach and for several scenarios. Just in the particular case where the outputs are proper, the pseudo-kernel cancels. Also, the hyperparameters of the covariance {can be learnt} maximizing the marginal likelihood using Wirtinger's calculus and patterned complex-valued matrix derivatives. In the experiments included, we show how CGPR successfully solve systems where real and imaginary parts are correlated. Besides, we successfully solve the nonlinear channel equalization problem by developing a recursive solution with basis removal. We report remarkable improvements compared to previous solutions: a 2-4 dB reduction of the MSE with {just a quarter} of the training samples used by previous approaches.

Proper Complex Gaussian Processes for Regression

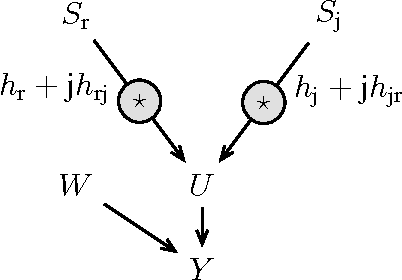
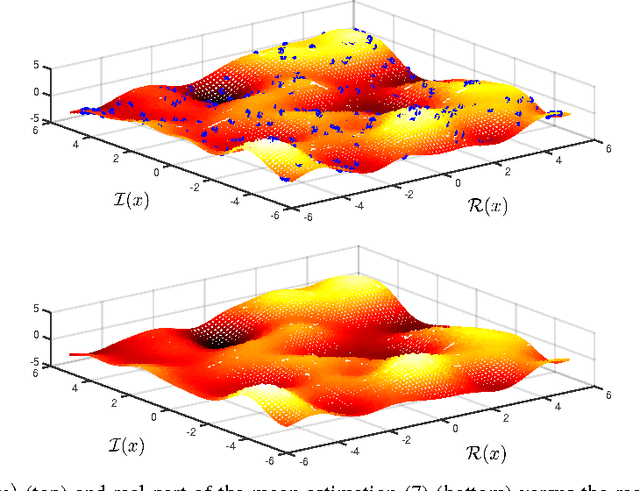
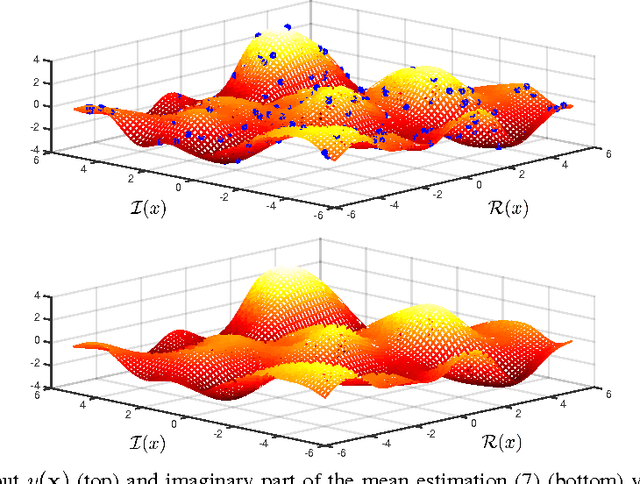
Complex-valued signals are used in the modeling of many systems in engineering and science, hence being of fundamental interest. Often, random complex-valued signals are considered to be proper. A proper complex random variable or process is uncorrelated with its complex conjugate. This assumption is a good model of the underlying physics in many problems, and simplifies the computations. While linear processing and neural networks have been widely studied for these signals, the development of complex-valued nonlinear kernel approaches remains an open problem. In this paper we propose Gaussian processes for regression as a framework to develop 1) a solution for proper complex-valued kernel regression and 2) the design of the reproducing kernel for complex-valued inputs, using the convolutional approach for cross-covariances. In this design we pay attention to preserve, in the complex domain, the measure of similarity between near inputs. The hyperparameters of the kernel are learned maximizing the marginal likelihood using Wirtinger derivatives. Besides, the approach is connected to the multiple output learning scenario. In the experiments included, we first solve a proper complex Gaussian process where the cross-covariance does not cancel, a challenging scenario when dealing with proper complex signals. Then we successfully use these novel results to solve some problems previously proposed in the literature as benchmarks, reporting a remarkable improvement in the estimation error.