Thread Counting in Plain Weave for Old Paintings Using Semi-Supervised Regression Deep Learning Models

In this work, the authors develop regression approaches based on deep learning to perform thread density estimation for plain weave canvas analysis. Previous approaches were based on Fourier analysis, which is quite robust for some scenarios but fails in some others, in machine learning tools, that involve pre-labeling of the painting at hand, or the segmentation of thread crossing points, that provides good estimations in all scenarios with no need of pre-labeling. The segmentation approach is time-consuming as the estimation of the densities is performed after locating the crossing points. In this novel proposal, we avoid this step by computing the density of threads directly from the image with a regression deep learning model. We also incorporate some improvements in the initial preprocessing of the input image with an impact on the final error. Several models are proposed and analyzed to retain the best one. Furthermore, we further reduce the density estimation error by introducing a semi-supervised approach. The performance of our novel algorithm is analyzed with works by Ribera, Vel\'azquez, and Poussin where we compare our results to the ones of previous approaches. Finally, the method is put into practice to support the change of authorship or a masterpiece at the Museo del Prado.

Complex-Valued Gaussian Processes for Regression

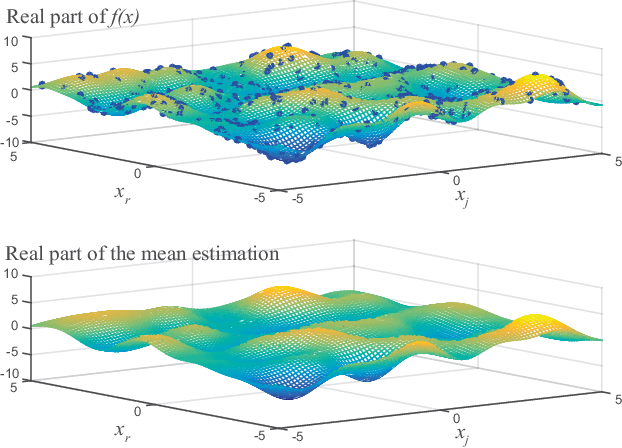
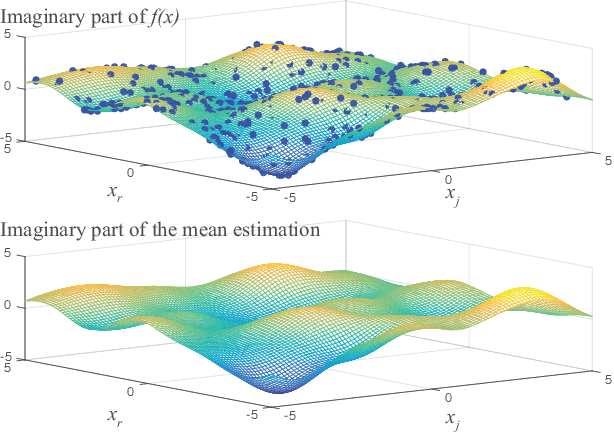
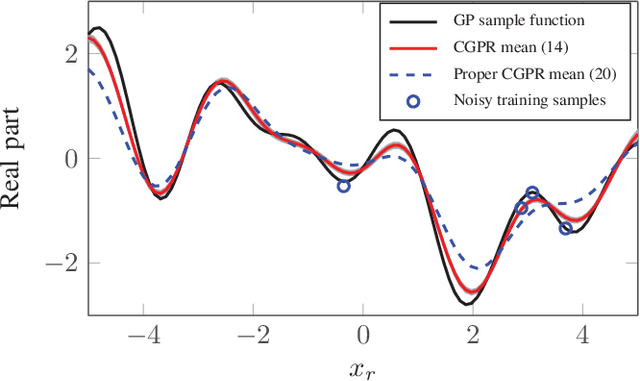
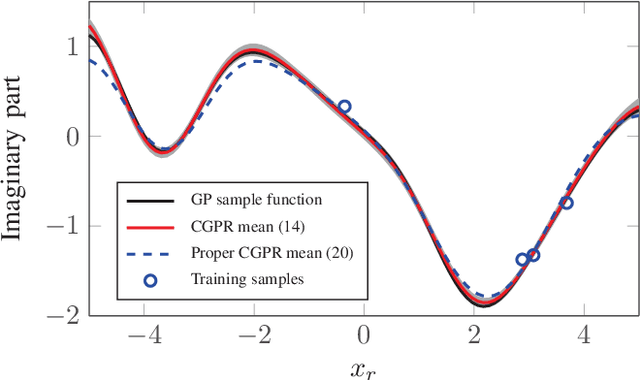
In this paper we propose a novel Bayesian solution for nonlinear regression in complex fields. Previous solutions for kernels methods usually assume a complexification approach, where the real-valued kernel is replaced by a complex-valued one. This approach is limited. Based on results in complex-valued linear theory and Gaussian random processes we show that a pseudo-kernel must be included. This is the starting point to develop the new complex-valued formulation for Gaussian process for regression (CGPR). We face the design of the covariance and pseudo-covariance based on a convolution approach and for several scenarios. Just in the particular case where the outputs are proper, the pseudo-kernel cancels. Also, the hyperparameters of the covariance {can be learnt} maximizing the marginal likelihood using Wirtinger's calculus and patterned complex-valued matrix derivatives. In the experiments included, we show how CGPR successfully solve systems where real and imaginary parts are correlated. Besides, we successfully solve the nonlinear channel equalization problem by developing a recursive solution with basis removal. We report remarkable improvements compared to previous solutions: a 2-4 dB reduction of the MSE with {just a quarter} of the training samples used by previous approaches.

On the Power Spectral Density Applied to the Analysis of Old Canvases

A routine task for art historians is painting diagnostics, such as dating or attribution. Signal processing of the X-ray image of a canvas provides useful information about its fabric. However, previous methods may fail when very old and deteriorated artworks or simply canvases of small size are studied. We present a new framework to analyze and further characterize the paintings from their radiographs. First, we start from a general analysis of lattices and provide new unifying results about the theoretical spectra of weaves. Then, we use these results to infer the main structure of the fabric, like the type of weave and the thread densities. We propose a practical estimation of these theoretical results from paintings with the averaged power spectral density (PSD), which provides a more robust tool. Furthermore, we found that the PSD provides a fingerprint that characterizes the whole canvas. We search and discuss some distinctive features we may find in that fingerprint. We apply these results to several masterpieces of the 17th and 18th centuries from the Museo Nacional del Prado to show that this approach yields accurate results in thread counting and is very useful for paintings comparison, even in situations where previous methods fail.