Joyce Jiyoung Whang
SAIF: A Comprehensive Framework for Evaluating the Risks of Generative AI in the Public Sector
Jan 15, 2025Abstract:The rapid adoption of generative AI in the public sector, encompassing diverse applications ranging from automated public assistance to welfare services and immigration processes, highlights its transformative potential while underscoring the pressing need for thorough risk assessments. Despite its growing presence, evaluations of risks associated with AI-driven systems in the public sector remain insufficiently explored. Building upon an established taxonomy of AI risks derived from diverse government policies and corporate guidelines, we investigate the critical risks posed by generative AI in the public sector while extending the scope to account for its multimodal capabilities. In addition, we propose a Systematic dAta generatIon Framework for evaluating the risks of generative AI (SAIF). SAIF involves four key stages: breaking down risks, designing scenarios, applying jailbreak methods, and exploring prompt types. It ensures the systematic and consistent generation of prompt data, facilitating a comprehensive evaluation while providing a solid foundation for mitigating the risks. Furthermore, SAIF is designed to accommodate emerging jailbreak methods and evolving prompt types, thereby enabling effective responses to unforeseen risk scenarios. We believe that this study can play a crucial role in fostering the safe and responsible integration of generative AI into the public sector.
Unveiling the Threat of Fraud Gangs to Graph Neural Networks: Multi-Target Graph Injection Attacks against GNN-Based Fraud Detectors
Dec 24, 2024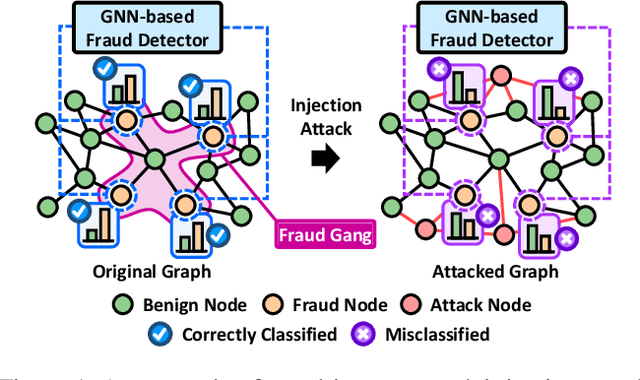

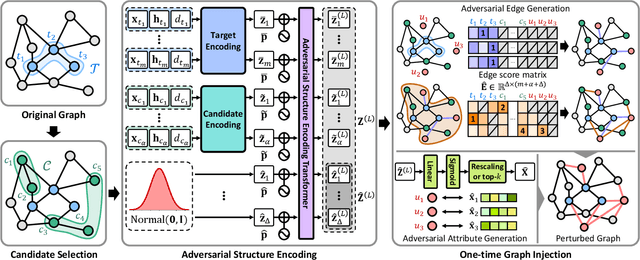

Abstract:Graph neural networks (GNNs) have emerged as an effective tool for fraud detection, identifying fraudulent users, and uncovering malicious behaviors. However, attacks against GNN-based fraud detectors and their risks have rarely been studied, thereby leaving potential threats unaddressed. Recent findings suggest that frauds are increasingly organized as gangs or groups. In this work, we design attack scenarios where fraud gangs aim to make their fraud nodes misclassified as benign by camouflaging their illicit activities in collusion. Based on these scenarios, we study adversarial attacks against GNN-based fraud detectors by simulating attacks of fraud gangs in three real-world fraud cases: spam reviews, fake news, and medical insurance frauds. We define these attacks as multi-target graph injection attacks and propose MonTi, a transformer-based Multi-target one-Time graph injection attack model. MonTi simultaneously generates attributes and edges of all attack nodes with a transformer encoder, capturing interdependencies between attributes and edges more effectively than most existing graph injection attack methods that generate these elements sequentially. Additionally, MonTi adaptively allocates the degree budget for each attack node to explore diverse injection structures involving target, candidate, and attack nodes, unlike existing methods that fix the degree budget across all attack nodes. Experiments show that MonTi outperforms the state-of-the-art graph injection attack methods on five real-world graphs.
SpoT-Mamba: Learning Long-Range Dependency on Spatio-Temporal Graphs with Selective State Spaces
Jun 17, 2024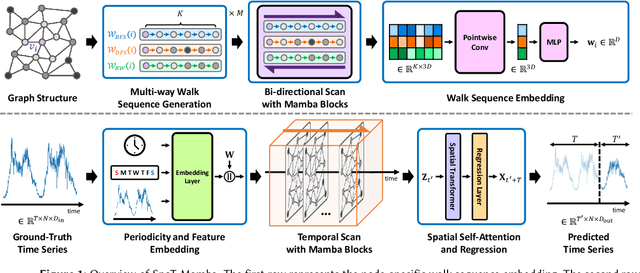

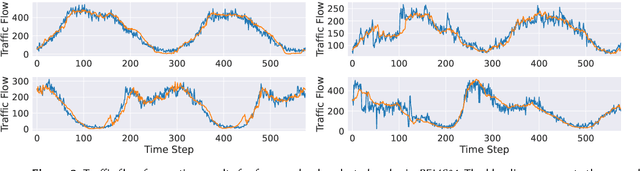
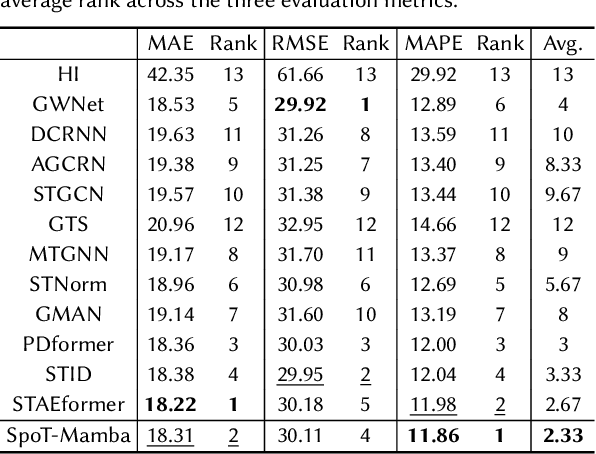
Abstract:Spatio-temporal graph (STG) forecasting is a critical task with extensive applications in the real world, including traffic and weather forecasting. Although several recent methods have been proposed to model complex dynamics in STGs, addressing long-range spatio-temporal dependencies remains a significant challenge, leading to limited performance gains. Inspired by a recently proposed state space model named Mamba, which has shown remarkable capability of capturing long-range dependency, we propose a new STG forecasting framework named SpoT-Mamba. SpoT-Mamba generates node embeddings by scanning various node-specific walk sequences. Based on the node embeddings, it conducts temporal scans to capture long-range spatio-temporal dependencies. Experimental results on the real-world traffic forecasting dataset demonstrate the effectiveness of SpoT-Mamba.
Dynamic Relation-Attentive Graph Neural Networks for Fraud Detection
Oct 09, 2023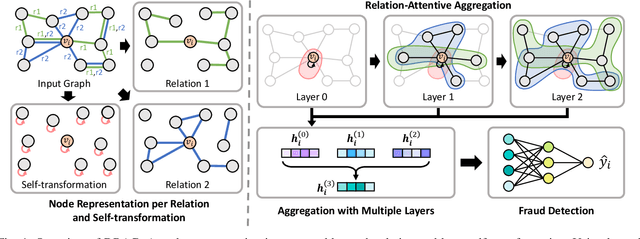
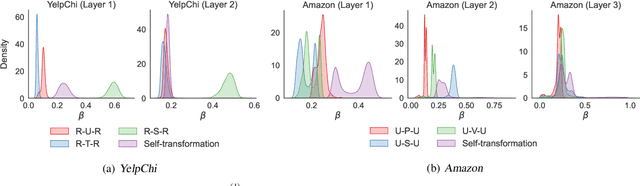
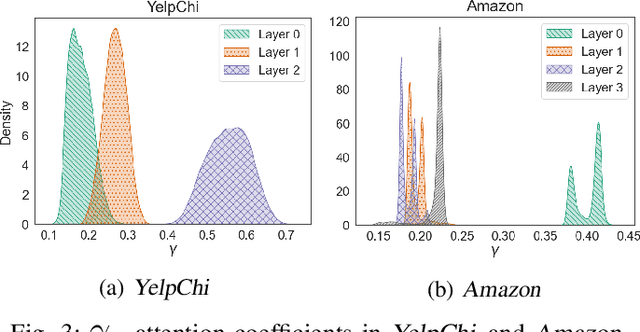
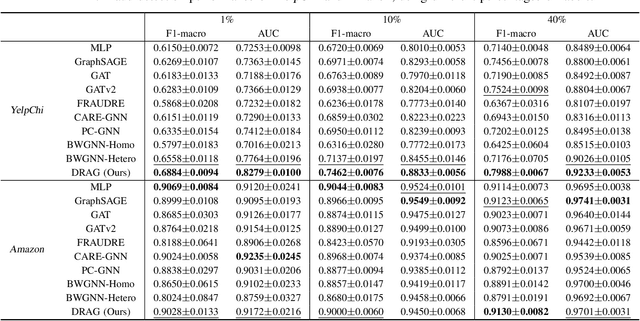
Abstract:Fraud detection aims to discover fraudsters deceiving other users by, for example, leaving fake reviews or making abnormal transactions. Graph-based fraud detection methods consider this task as a classification problem with two classes: frauds or normal. We address this problem using Graph Neural Networks (GNNs) by proposing a dynamic relation-attentive aggregation mechanism. Based on the observation that many real-world graphs include different types of relations, we propose to learn a node representation per relation and aggregate the node representations using a learnable attention function that assigns a different attention coefficient to each relation. Furthermore, we combine the node representations from different layers to consider both the local and global structures of a target node, which is beneficial to improving the performance of fraud detection on graphs with heterophily. By employing dynamic graph attention in all the aggregation processes, our method adaptively computes the attention coefficients for each node. Experimental results show that our method, DRAG, outperforms state-of-the-art fraud detection methods on real-world benchmark datasets.
Representation Learning on Hyper-Relational and Numeric Knowledge Graphs with Transformers
Jun 01, 2023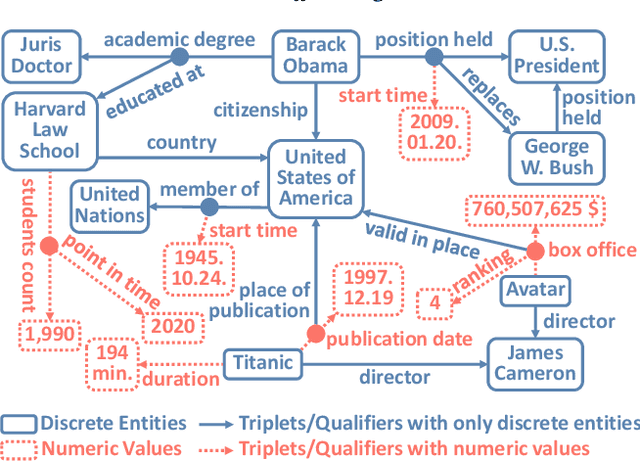
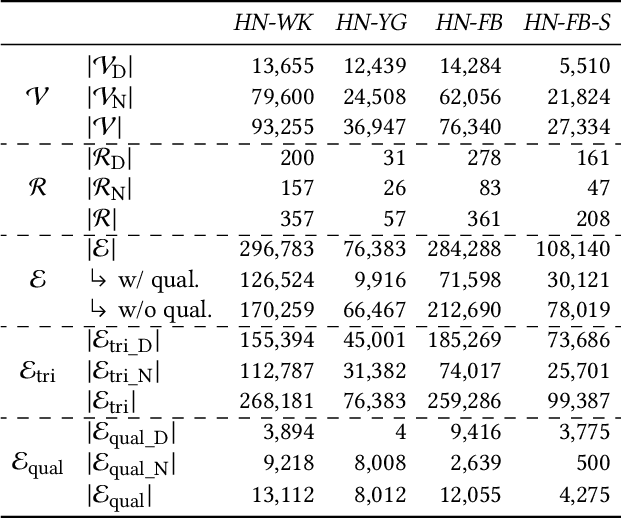
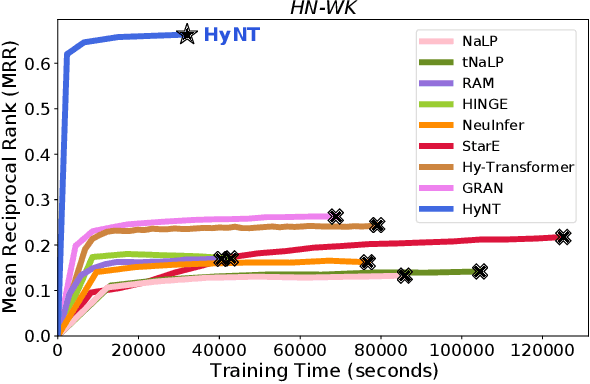
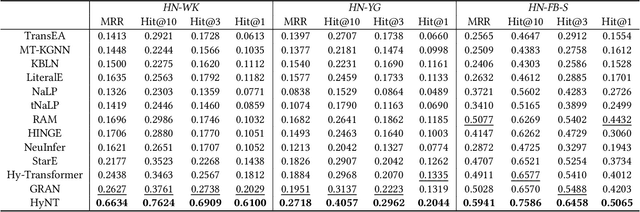
Abstract:A hyper-relational knowledge graph has been recently studied where a triplet is associated with a set of qualifiers; a qualifier is composed of a relation and an entity, providing auxiliary information for a triplet. While existing hyper-relational knowledge graph embedding methods assume that the entities are discrete objects, some information should be represented using numeric values, e.g., (J.R.R., was born in, 1892). Also, a triplet (J.R.R., educated at, Oxford Univ.) can be associated with a qualifier such as (start time, 1911). In this paper, we propose a unified framework named HyNT that learns representations of a hyper-relational knowledge graph containing numeric literals in either triplets or qualifiers. We define a context transformer and a prediction transformer to learn the representations based not only on the correlations between a triplet and its qualifiers but also on the numeric information. By learning compact representations of triplets and qualifiers and feeding them into the transformers, we reduce the computation cost of using transformers. Using HyNT, we can predict missing numeric values in addition to missing entities or relations in a hyper-relational knowledge graph. Experimental results show that HyNT significantly outperforms state-of-the-art methods on real-world datasets.
InGram: Inductive Knowledge Graph Embedding via Relation Graphs
Jun 01, 2023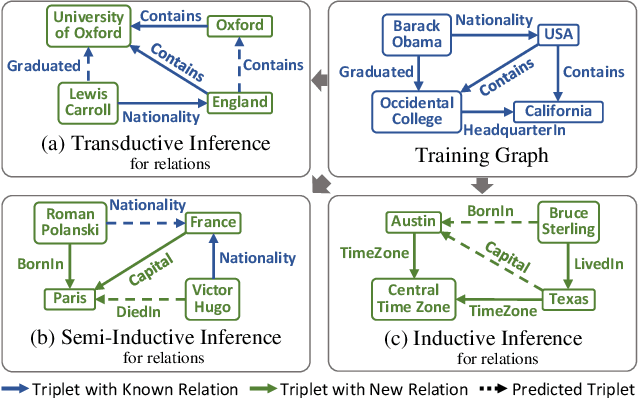
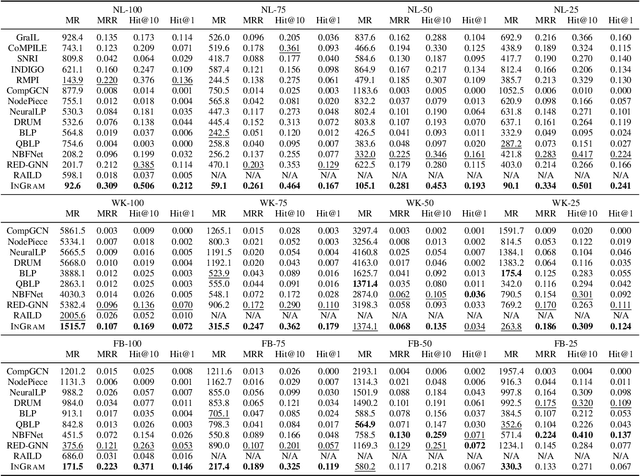
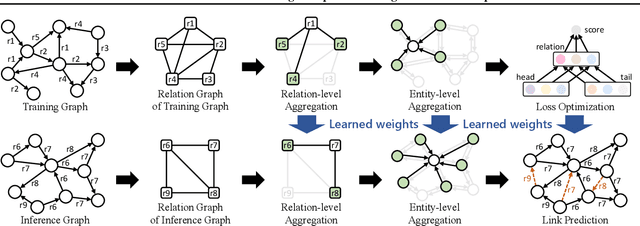
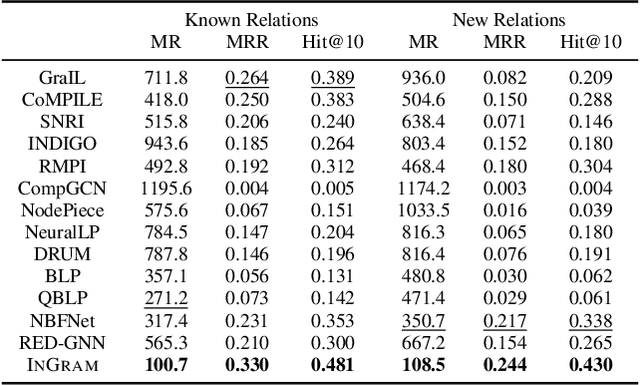
Abstract:Inductive knowledge graph completion has been considered as the task of predicting missing triplets between new entities that are not observed during training. While most inductive knowledge graph completion methods assume that all entities can be new, they do not allow new relations to appear at inference time. This restriction prohibits the existing methods from appropriately handling real-world knowledge graphs where new entities accompany new relations. In this paper, we propose an INductive knowledge GRAph eMbedding method, InGram, that can generate embeddings of new relations as well as new entities at inference time. Given a knowledge graph, we define a relation graph as a weighted graph consisting of relations and the affinity weights between them. Based on the relation graph and the original knowledge graph, InGram learns how to aggregate neighboring embeddings to generate relation and entity embeddings using an attention mechanism. Experimental results show that InGram outperforms 14 different state-of-the-art methods on varied inductive learning scenarios.
Discern and Answer: Mitigating the Impact of Misinformation in Retrieval-Augmented Models with Discriminators
May 02, 2023Abstract:Most existing retrieval-augmented language models (LMs) for question answering assume all retrieved information is factually correct. In this work, we study a more realistic scenario in which retrieved documents may contain misinformation, causing conflicts among them. We observe that the existing models are highly brittle to such information in both fine-tuning and in-context few-shot learning settings. We propose approaches to make retrieval-augmented LMs robust to misinformation by explicitly fine-tuning a discriminator or prompting to elicit discrimination capability in GPT-3. Our empirical results on open-domain question answering show that these approaches significantly improve LMs' robustness to knowledge conflicts. We also provide our findings on interleaving the fine-tuned model's decision with the in-context learning process, paving a new path to leverage the best of both worlds.
Learning Representations of Bi-Level Knowledge Graphs for Reasoning beyond Link Prediction
Feb 06, 2023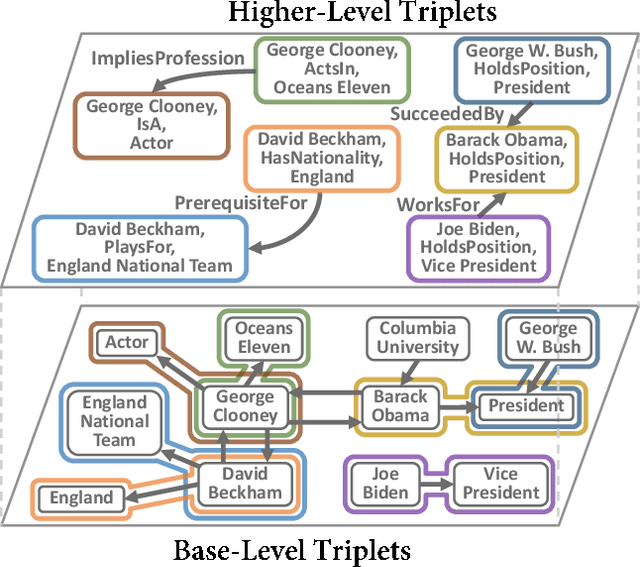

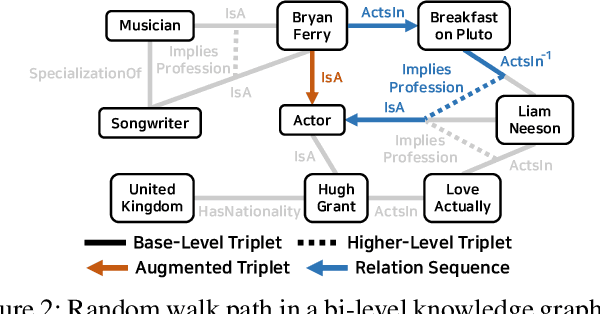
Abstract:Knowledge graphs represent known facts using triplets. While existing knowledge graph embedding methods only consider the connections between entities, we propose considering the relationships between triplets. For example, let us consider two triplets $T_1$ and $T_2$ where $T_1$ is (Academy_Awards, Nominates, Avatar) and $T_2$ is (Avatar, Wins, Academy_Awards). Given these two base-level triplets, we see that $T_1$ is a prerequisite for $T_2$. In this paper, we define a higher-level triplet to represent a relationship between triplets, e.g., $\langle T_1$, PrerequisiteFor, $T_2\rangle$ where PrerequisiteFor is a higher-level relation. We define a bi-level knowledge graph that consists of the base-level and the higher-level triplets. We also propose a data augmentation strategy based on the random walks on the bi-level knowledge graph to augment plausible triplets. Our model called BiVE learns embeddings by taking into account the structures of the base-level and the higher-level triplets, with additional consideration of the augmented triplets. We propose two new tasks: triplet prediction and conditional link prediction. Given a triplet $T_1$ and a higher-level relation, the triplet prediction predicts a triplet that is likely to be connected to $T_1$ by the higher-level relation, e.g., $\langle T_1$, PrerequisiteFor, ?$\rangle$. The conditional link prediction predicts a missing entity in a triplet conditioned on another triplet, e.g., $\langle T_1$, PrerequisiteFor, (Avatar, Wins, ?)$\rangle$. Experimental results show that BiVE significantly outperforms all other methods in the two new tasks and the typical base-level link prediction in real-world bi-level knowledge graphs.
Non-Exhaustive, Overlapping Co-Clustering: An Extended Analysis
Apr 24, 2020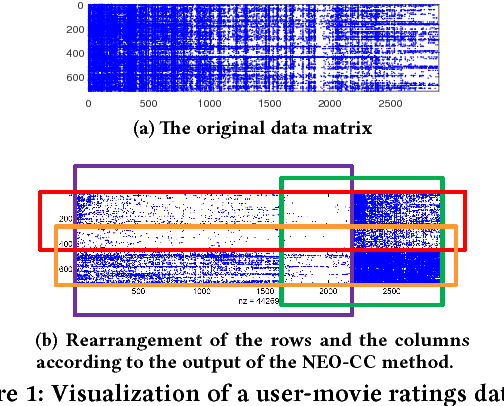
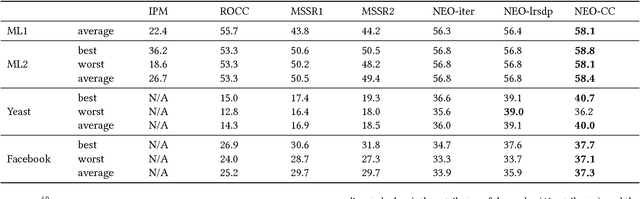
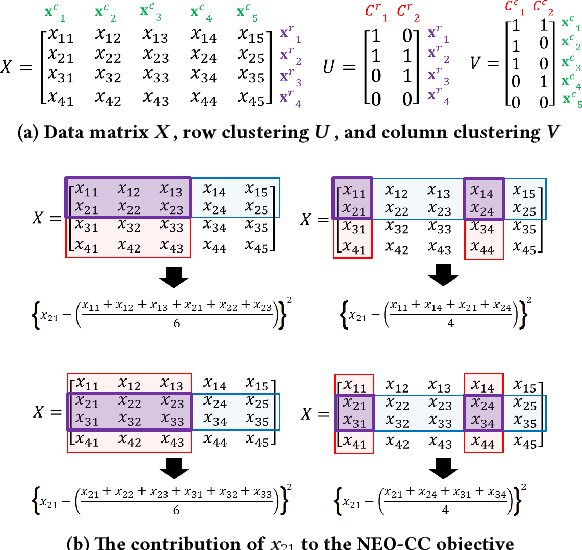
Abstract:The goal of co-clustering is to simultaneously identify a clustering of rows as well as columns of a two dimensional data matrix. A number of co-clustering techniques have been proposed including information-theoretic co-clustering and the minimum sum-squared residue co-clustering method. However, most existing co-clustering algorithms are designed to find pairwise disjoint and exhaustive co-clusters while many real-world datasets contain not only a large overlap between co-clusters but also outliers which should not belong to any co-cluster. In this paper, we formulate the problem of Non-Exhaustive, Overlapping Co-Clustering where both of the row and column clusters are allowed to overlap with each other and outliers for each dimension of the data matrix are not assigned to any cluster. To solve this problem, we propose intuitive objective functions, and develop an an efficient iterative algorithm which we call the NEO-CC algorithm. We theoretically show that the NEO-CC algorithm monotonically decreases the proposed objective functions. Experimental results show that the NEO-CC algorithm is able to effectively capture the underlying co-clustering structure of real-world data, and thus outperforms state-of-the-art clustering and co-clustering methods. This manuscript includes an extended analysis of [21].
Fast Multiplier Methods to Optimize Non-exhaustive, Overlapping Clustering
Feb 05, 2016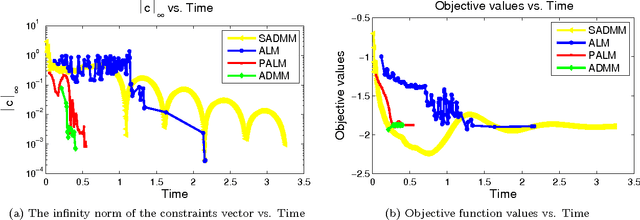
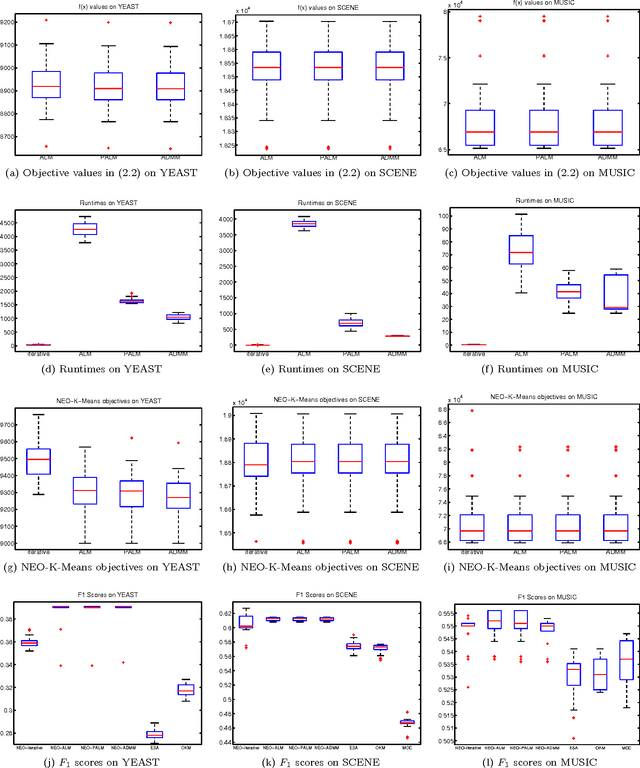
Abstract:Clustering is one of the most fundamental and important tasks in data mining. Traditional clustering algorithms, such as K-means, assign every data point to exactly one cluster. However, in real-world datasets, the clusters may overlap with each other. Furthermore, often, there are outliers that should not belong to any cluster. We recently proposed the NEO-K-Means (Non-Exhaustive, Overlapping K-Means) objective as a way to address both issues in an integrated fashion. Optimizing this discrete objective is NP-hard, and even though there is a convex relaxation of the objective, straightforward convex optimization approaches are too expensive for large datasets. A practical alternative is to use a low-rank factorization of the solution matrix in the convex formulation. The resulting optimization problem is non-convex, and we can locally optimize the objective function using an augmented Lagrangian method. In this paper, we consider two fast multiplier methods to accelerate the convergence of an augmented Lagrangian scheme: a proximal method of multipliers and an alternating direction method of multipliers (ADMM). For the proximal augmented Lagrangian or proximal method of multipliers, we show a convergence result for the non-convex case with bound-constrained subproblems. These methods are up to 13 times faster---with no change in quality---compared with a standard augmented Lagrangian method on problems with over 10,000 variables and bring runtimes down from over an hour to around 5 minutes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge