Fast Multiplier Methods to Optimize Non-exhaustive, Overlapping Clustering
Paper and Code
Feb 05, 2016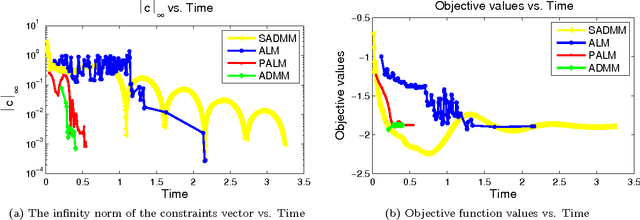
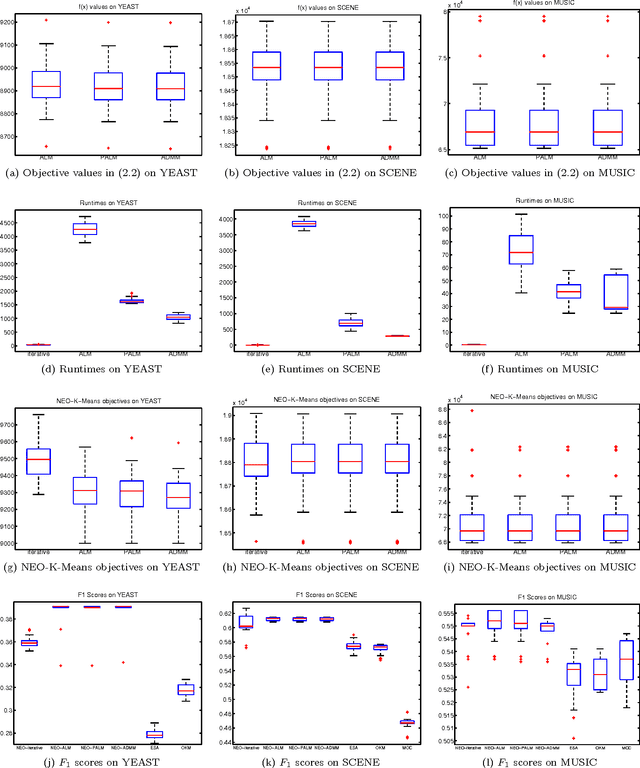
Clustering is one of the most fundamental and important tasks in data mining. Traditional clustering algorithms, such as K-means, assign every data point to exactly one cluster. However, in real-world datasets, the clusters may overlap with each other. Furthermore, often, there are outliers that should not belong to any cluster. We recently proposed the NEO-K-Means (Non-Exhaustive, Overlapping K-Means) objective as a way to address both issues in an integrated fashion. Optimizing this discrete objective is NP-hard, and even though there is a convex relaxation of the objective, straightforward convex optimization approaches are too expensive for large datasets. A practical alternative is to use a low-rank factorization of the solution matrix in the convex formulation. The resulting optimization problem is non-convex, and we can locally optimize the objective function using an augmented Lagrangian method. In this paper, we consider two fast multiplier methods to accelerate the convergence of an augmented Lagrangian scheme: a proximal method of multipliers and an alternating direction method of multipliers (ADMM). For the proximal augmented Lagrangian or proximal method of multipliers, we show a convergence result for the non-convex case with bound-constrained subproblems. These methods are up to 13 times faster---with no change in quality---compared with a standard augmented Lagrangian method on problems with over 10,000 variables and bring runtimes down from over an hour to around 5 minutes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge