Learning Representations of Bi-Level Knowledge Graphs for Reasoning beyond Link Prediction
Paper and Code
Feb 06, 2023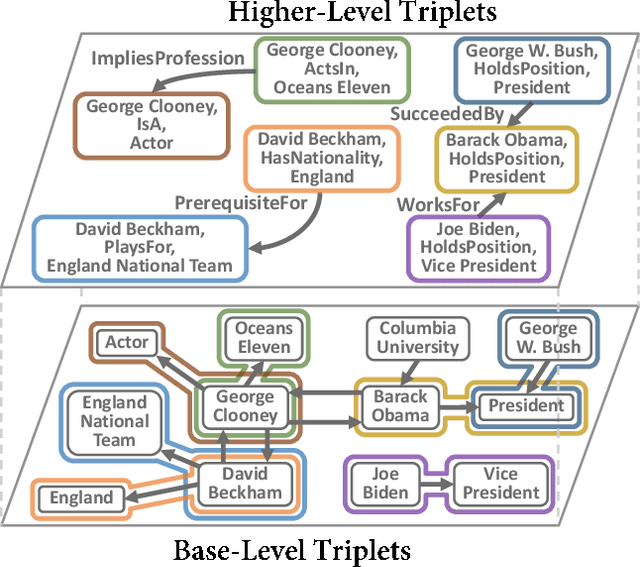

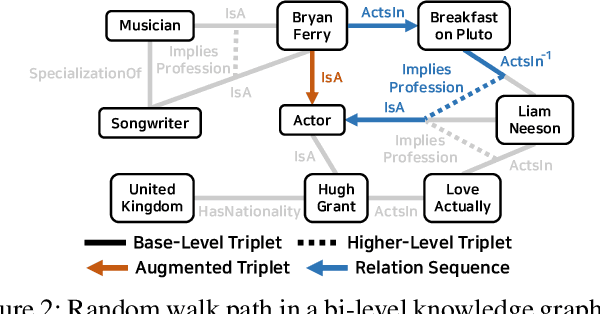
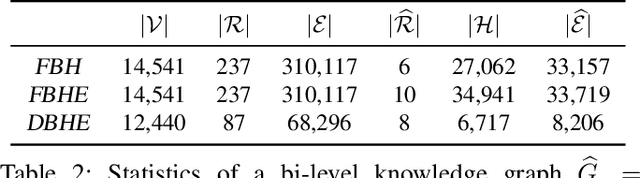
Knowledge graphs represent known facts using triplets. While existing knowledge graph embedding methods only consider the connections between entities, we propose considering the relationships between triplets. For example, let us consider two triplets $T_1$ and $T_2$ where $T_1$ is (Academy_Awards, Nominates, Avatar) and $T_2$ is (Avatar, Wins, Academy_Awards). Given these two base-level triplets, we see that $T_1$ is a prerequisite for $T_2$. In this paper, we define a higher-level triplet to represent a relationship between triplets, e.g., $\langle T_1$, PrerequisiteFor, $T_2\rangle$ where PrerequisiteFor is a higher-level relation. We define a bi-level knowledge graph that consists of the base-level and the higher-level triplets. We also propose a data augmentation strategy based on the random walks on the bi-level knowledge graph to augment plausible triplets. Our model called BiVE learns embeddings by taking into account the structures of the base-level and the higher-level triplets, with additional consideration of the augmented triplets. We propose two new tasks: triplet prediction and conditional link prediction. Given a triplet $T_1$ and a higher-level relation, the triplet prediction predicts a triplet that is likely to be connected to $T_1$ by the higher-level relation, e.g., $\langle T_1$, PrerequisiteFor, ?$\rangle$. The conditional link prediction predicts a missing entity in a triplet conditioned on another triplet, e.g., $\langle T_1$, PrerequisiteFor, (Avatar, Wins, ?)$\rangle$. Experimental results show that BiVE significantly outperforms all other methods in the two new tasks and the typical base-level link prediction in real-world bi-level knowledge graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge