Non-Exhaustive, Overlapping Co-Clustering: An Extended Analysis
Paper and Code
Apr 24, 2020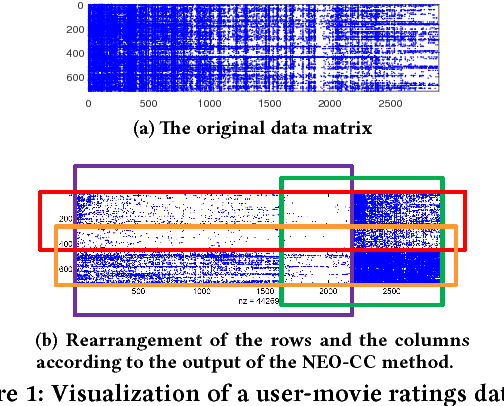
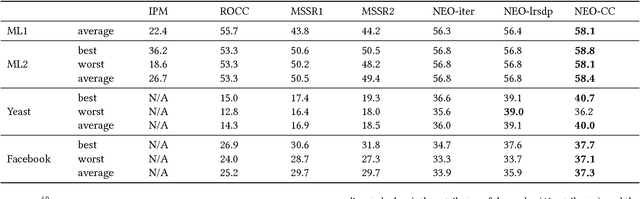
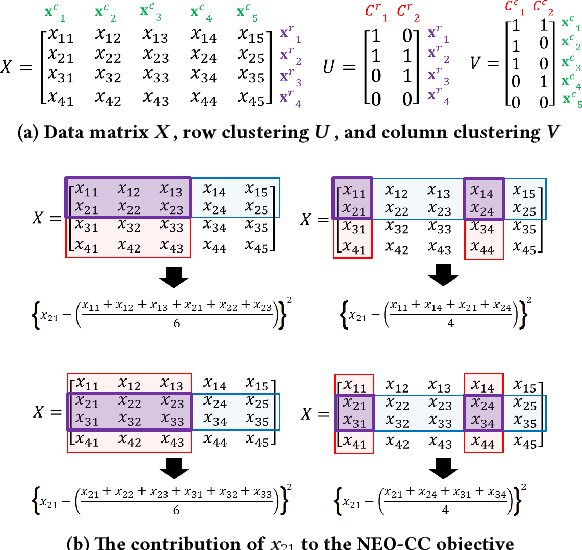
The goal of co-clustering is to simultaneously identify a clustering of rows as well as columns of a two dimensional data matrix. A number of co-clustering techniques have been proposed including information-theoretic co-clustering and the minimum sum-squared residue co-clustering method. However, most existing co-clustering algorithms are designed to find pairwise disjoint and exhaustive co-clusters while many real-world datasets contain not only a large overlap between co-clusters but also outliers which should not belong to any co-cluster. In this paper, we formulate the problem of Non-Exhaustive, Overlapping Co-Clustering where both of the row and column clusters are allowed to overlap with each other and outliers for each dimension of the data matrix are not assigned to any cluster. To solve this problem, we propose intuitive objective functions, and develop an an efficient iterative algorithm which we call the NEO-CC algorithm. We theoretically show that the NEO-CC algorithm monotonically decreases the proposed objective functions. Experimental results show that the NEO-CC algorithm is able to effectively capture the underlying co-clustering structure of real-world data, and thus outperforms state-of-the-art clustering and co-clustering methods. This manuscript includes an extended analysis of [21].
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge