Explainable Unsupervised Anomaly Detection with Random Forest

We describe the use of an unsupervised Random Forest for similarity learning and improved unsupervised anomaly detection. By training a Random Forest to discriminate between real data and synthetic data sampled from a uniform distribution over the real data bounds, a distance measure is obtained that anisometrically transforms the data, expanding distances at the boundary of the data manifold. We show that using distances recovered from this transformation improves the accuracy of unsupervised anomaly detection, compared to other commonly used detectors, demonstrated over a large number of benchmark datasets. As well as improved performance, this method has advantages over other unsupervised anomaly detection methods, including minimal requirements for data preprocessing, native handling of missing data, and potential for visualizations. By relating outlier scores to partitions of the Random Forest, we develop a method for locally explainable anomaly predictions in terms of feature importance.

Supervised Similarity for High-Yield Corporate Bonds with Quantum Cognition Machine Learning

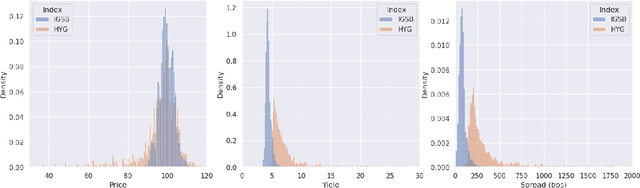
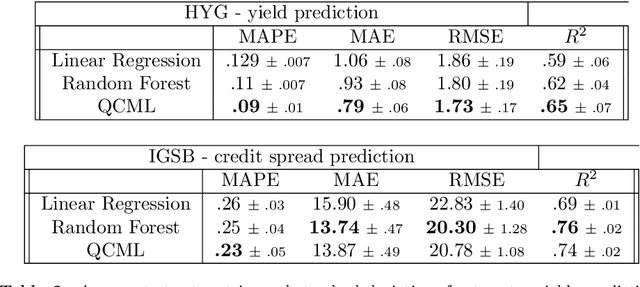
We investigate the application of quantum cognition machine learning (QCML), a novel paradigm for both supervised and unsupervised learning tasks rooted in the mathematical formalism of quantum theory, to distance metric learning in corporate bond markets. Compared to equities, corporate bonds are relatively illiquid and both trade and quote data in these securities are relatively sparse. Thus, a measure of distance/similarity among corporate bonds is particularly useful for a variety of practical applications in the trading of illiquid bonds, including the identification of similar tradable alternatives, pricing securities with relatively few recent quotes or trades, and explaining the predictions and performance of ML models based on their training data. Previous research has explored supervised similarity learning based on classical tree-based models in this context; here, we explore the application of the QCML paradigm for supervised distance metric learning in the same context, showing that it outperforms classical tree-based models in high-yield (HY) markets, while giving comparable or better performance (depending on the evaluation metric) in investment grade (IG) markets.

Quantile Regression using Random Forest Proximities

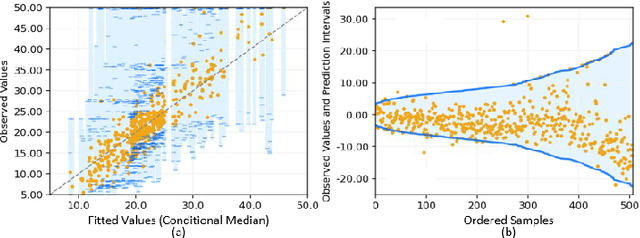
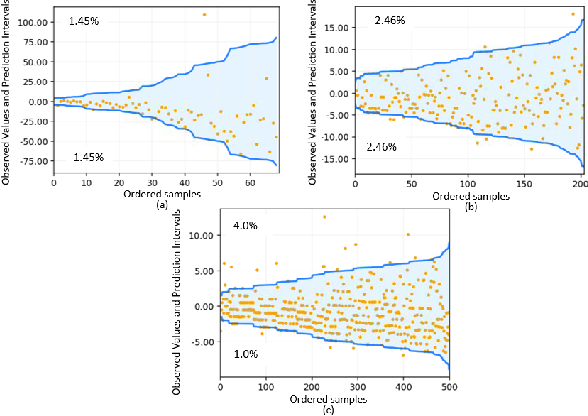
Due to the dynamic nature of financial markets, maintaining models that produce precise predictions over time is difficult. Often the goal isn't just point prediction but determining uncertainty. Quantifying uncertainty, especially the aleatoric uncertainty due to the unpredictable nature of market drivers, helps investors understand varying risk levels. Recently, quantile regression forests (QRF) have emerged as a promising solution: Unlike most basic quantile regression methods that need separate models for each quantile, quantile regression forests estimate the entire conditional distribution of the target variable with a single model, while retaining all the salient features of a typical random forest. We introduce a novel approach to compute quantile regressions from random forests that leverages the proximity (i.e., distance metric) learned by the model and infers the conditional distribution of the target variable. We evaluate the proposed methodology using publicly available datasets and then apply it towards the problem of forecasting the average daily volume of corporate bonds. We show that using quantile regression using Random Forest proximities demonstrates superior performance in approximating conditional target distributions and prediction intervals to the original version of QRF. We also demonstrate that the proposed framework is significantly more computationally efficient than traditional approaches to quantile regressions.

Towards Enhanced Local Explainability of Random Forests: a Proximity-Based Approach

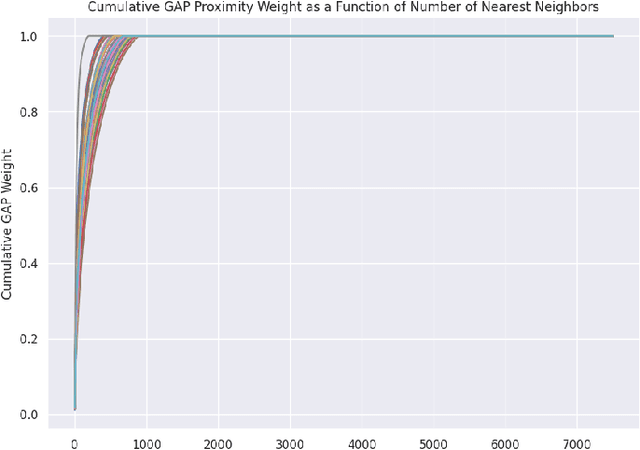
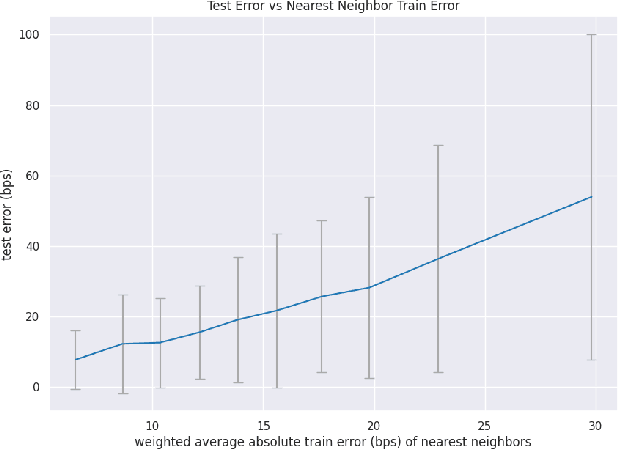
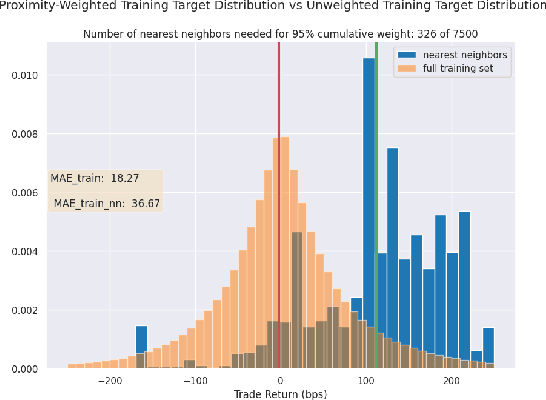
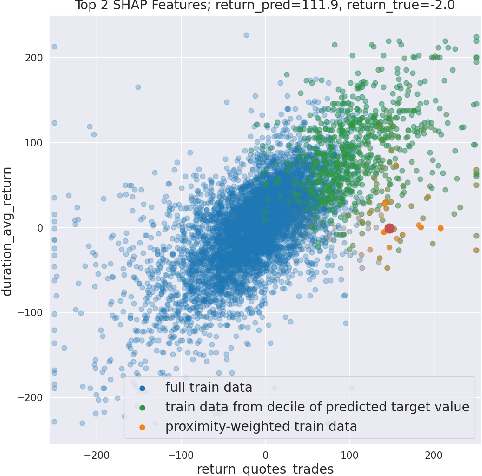
We initiate a novel approach to explain the out of sample performance of random forest (RF) models by exploiting the fact that any RF can be formulated as an adaptive weighted K nearest-neighbors model. Specifically, we use the proximity between points in the feature space learned by the RF to re-write random forest predictions exactly as a weighted average of the target labels of training data points. This linearity facilitates a local notion of explainability of RF predictions that generates attributions for any model prediction across observations in the training set, and thereby complements established methods like SHAP, which instead generates attributions for a model prediction across dimensions of the feature space. We demonstrate this approach in the context of a bond pricing model trained on US corporate bond trades, and compare our approach to various existing approaches to model explainability.