How to Choose a Threshold for an Evaluation Metric for Large Language Models

To ensure and monitor large language models (LLMs) reliably, various evaluation metrics have been proposed in the literature. However, there is little research on prescribing a methodology to identify a robust threshold on these metrics even though there are many serious implications of an incorrect choice of the thresholds during deployment of the LLMs. Translating the traditional model risk management (MRM) guidelines within regulated industries such as the financial industry, we propose a step-by-step recipe for picking a threshold for a given LLM evaluation metric. We emphasize that such a methodology should start with identifying the risks of the LLM application under consideration and risk tolerance of the stakeholders. We then propose concrete and statistically rigorous procedures to determine a threshold for the given LLM evaluation metric using available ground-truth data. As a concrete example to demonstrate the proposed methodology at work, we employ it on the Faithfulness metric, as implemented in various publicly available libraries, using the publicly available HaluBench dataset. We also lay a foundation for creating systematic approaches to select thresholds, not only for LLMs but for any GenAI applications.

Case-based Explainability for Random Forest: Prototypes, Critics, Counter-factuals and Semi-factuals

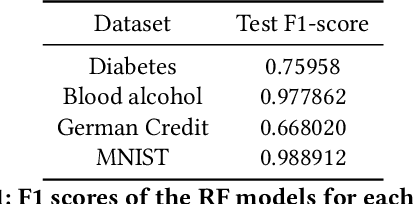
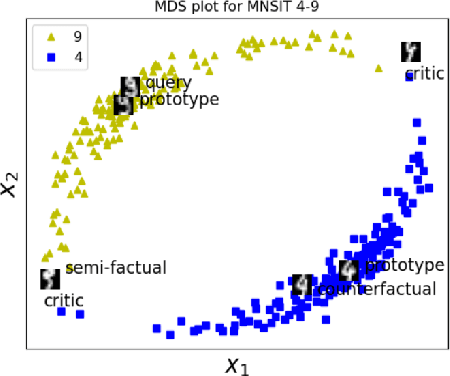
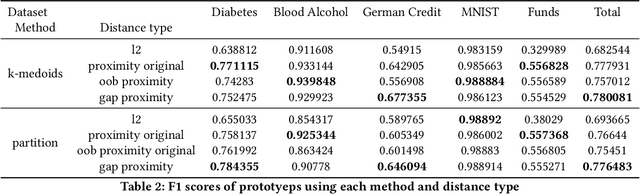
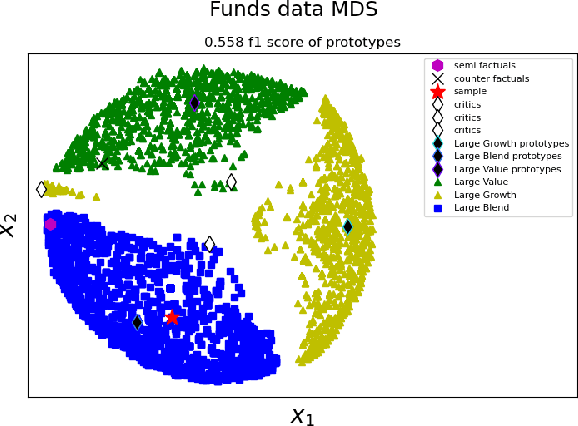
The explainability of black-box machine learning algorithms, commonly known as Explainable Artificial Intelligence (XAI), has become crucial for financial and other regulated industrial applications due to regulatory requirements and the need for transparency in business practices. Among the various paradigms of XAI, Explainable Case-Based Reasoning (XCBR) stands out as a pragmatic approach that elucidates the output of a model by referencing actual examples from the data used to train or test the model. Despite its potential, XCBR has been relatively underexplored for many algorithms such as tree-based models until recently. We start by observing that most XCBR methods are defined based on the distance metric learned by the algorithm. By utilizing a recently proposed technique to extract the distance metric learned by Random Forests (RFs), which is both geometry- and accuracy-preserving, we investigate various XCBR methods. These methods amount to identify special points from the training datasets, such as prototypes, critics, counter-factuals, and semi-factuals, to explain the predictions for a given query of the RF. We evaluate these special points using various evaluation metrics to assess their explanatory power and effectiveness.

Quantile Regression using Random Forest Proximities

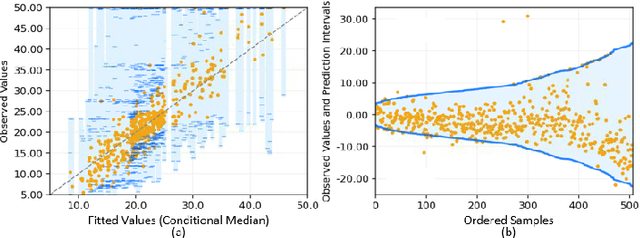
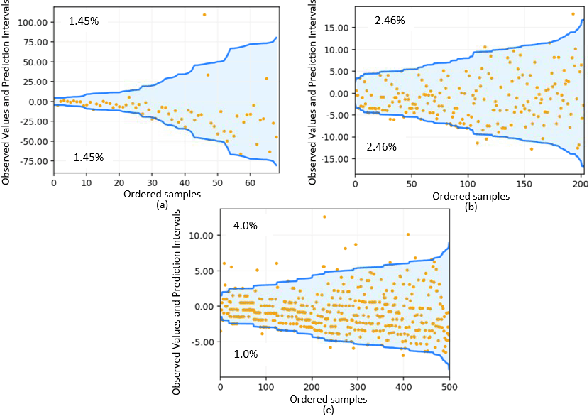
Due to the dynamic nature of financial markets, maintaining models that produce precise predictions over time is difficult. Often the goal isn't just point prediction but determining uncertainty. Quantifying uncertainty, especially the aleatoric uncertainty due to the unpredictable nature of market drivers, helps investors understand varying risk levels. Recently, quantile regression forests (QRF) have emerged as a promising solution: Unlike most basic quantile regression methods that need separate models for each quantile, quantile regression forests estimate the entire conditional distribution of the target variable with a single model, while retaining all the salient features of a typical random forest. We introduce a novel approach to compute quantile regressions from random forests that leverages the proximity (i.e., distance metric) learned by the model and infers the conditional distribution of the target variable. We evaluate the proposed methodology using publicly available datasets and then apply it towards the problem of forecasting the average daily volume of corporate bonds. We show that using quantile regression using Random Forest proximities demonstrates superior performance in approximating conditional target distributions and prediction intervals to the original version of QRF. We also demonstrate that the proposed framework is significantly more computationally efficient than traditional approaches to quantile regressions.