A Reinforcement Learning Approach to Quiet and Safe UAM Traffic Management

Urban air mobility (UAM) is a transformative system that operates various small aerial vehicles in urban environments to reshape urban transportation. However, integrating UAM into existing urban environments presents a variety of complex challenges. Recent analyses of UAM's operational constraints highlight aircraft noise and system safety as key hurdles to UAM system implementation. Future UAM air traffic management schemes must ensure that the system is both quiet and safe. We propose a multi-agent reinforcement learning approach to manage UAM traffic, aiming at both vertical separation assurance and noise mitigation. Through extensive training, the reinforcement learning agent learns to balance the two primary objectives by employing altitude adjustments in a multi-layer UAM network. The results reveal the tradeoffs among noise impact, traffic congestion, and separation. Overall, our findings demonstrate the potential of reinforcement learning in mitigating UAM's noise impact while maintaining safe separation using altitude adjustments

Cluster & Disperse: a general air conflict resolution heuristic using unsupervised learning

We provide a general and malleable heuristic for the air conflict resolution problem. This heuristic is based on a new neighborhood structure for searching the solution space of trajectories and flight-levels. Using unsupervised learning, the core idea of our heuristic is to cluster the conflict points and disperse them in various flight levels. Our first algorithm is called Cluster & Disperse and in each iteration it assigns the most problematic flights in each cluster to another flight-level. In effect, we shuffle them between the flight-levels until we achieve a well-balanced configuration. The Cluster & Disperse algorithm then uses any horizontal plane conflict resolution algorithm as a subroutine to solve these well-balanced instances. Nevertheless, we develop a novel algorithm for the horizontal plane based on a similar idea. That is we cluster and disperse the conflict points spatially in the same flight level using the gradient descent and a social force. We use a novel maneuver making flights travel on an arc instead of a straight path which is based on the aviation routine of the Radius to Fix legs. Our algorithms can handle a high density of flights within a reasonable computation time. We put their performance in context with some notable algorithms from the literature. Being a general framework, a particular strength of the Cluster & Disperse is its malleability in allowing various constraints regarding the aircraft or the environment to be integrated with ease. This is in contrast to the models for instance based on mixed integer programming.

Nested Vehicle Routing Problem: Optimizing Drone-Truck Surveillance Operations

Unmanned aerial vehicles or drones are becoming increasingly popular due to their low cost and high mobility. In this paper we address the routing and coordination of a drone-truck pairing where the drone travels to multiple locations to perform specified observation tasks and rendezvous periodically with the truck to swap its batteries. We refer to this as the Nested-Vehicle Routing Problem (Nested-VRP) and develop a Mixed Integer Programming (MIP) formulation with critical operational constraints, including drone battery capacity and synchronization of both vehicles during scheduled rendezvous. Given the NP-hard nature of the Nested-VRP, we propose an efficient neighborhood search (NS) heuristic where we generate and improve on a good initial solution (i.e., where the optimality gap is on average less than 6% in large instances) by iteratively solving the Nested-VRP on a local scale. We provide comparisons of both the MIP and NS heuristic methods with a relaxation lower bound in the cases of small and large problem sizes, and present the results of a computational study to show the effectiveness of the MIP model and the efficiency of the NS heuristic, including for a real-life instance with 631 locations. We envision that this framework will facilitate the planning and operations of combined drone-truck missions.

Finite-Time Analysis of Q-Learning with Linear Function Approximation

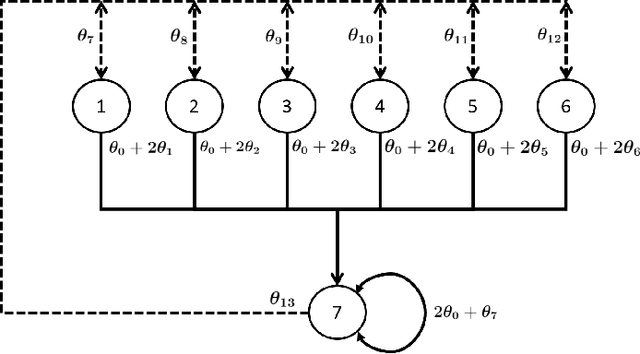
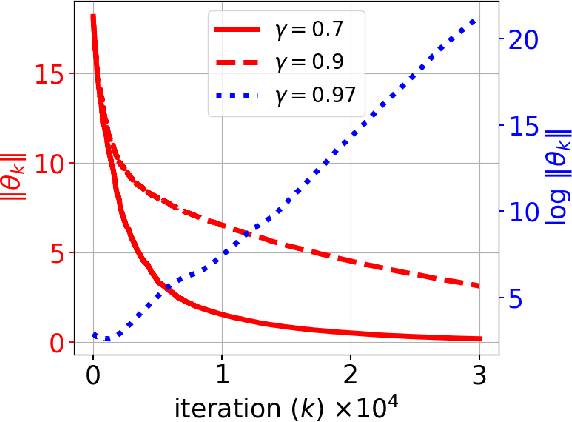
In this paper, we consider the model-free reinforcement learning problem and study the popular Q-learning algorithm with linear function approximation for finding the optimal policy. Despite its popularity, it is known that Q-learning with linear function approximation may diverge in general due to off-policy sampling. Our main contribution is to provide a finite-time bound for the performance of Q-learning with linear function approximation with constant step size under an assumption on the sampling policy. Unlike some prior work in the literature, we do not need to make the unnatural assumption that the samples are i.i.d. (since they are Markovian), and do not require an additional projection step in the algorithm. To show this result, we first consider a more general nonlinear stochastic approximation algorithm with Markovian noise, and derive a finite-time bound on the mean-square error, which we believe is of independent interest. Our proof is based on Lyapunov drift arguments and exploits the geometric mixing of the underlying Markov chain. We also provide numerical simulations to illustrate the effectiveness of our assumption on the sampling policy, and demonstrate the rate of convergence of Q-learning.

Airport Gate Scheduling for Passengers, Aircraft, and Operation

Passengers' experience is becoming a key metric to evaluate the air transportation system's performance. Efficient and robust tools to handle airport operations are needed along with a better understanding of passengers' interests and concerns. Among various airport operations, this paper studies airport gate scheduling for improved passengers' experience. Three objectives accounting for passengers, aircraft, and operation are presented. Trade-offs between these objectives are analyzed, and a balancing objective function is proposed. The results show that the balanced objective can improve the efficiency of traffic flow in passenger terminals and on ramps, as well as the robustness of gate operations.