Finite-Time Analysis of Q-Learning with Linear Function Approximation

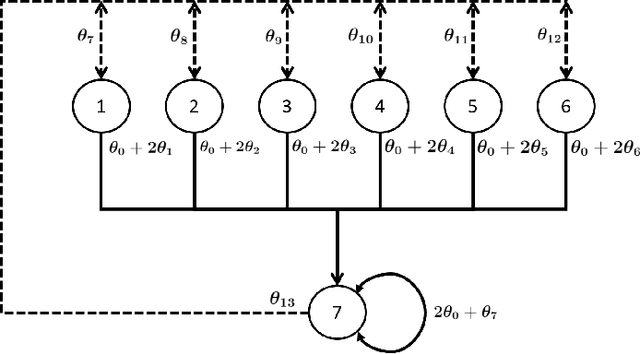
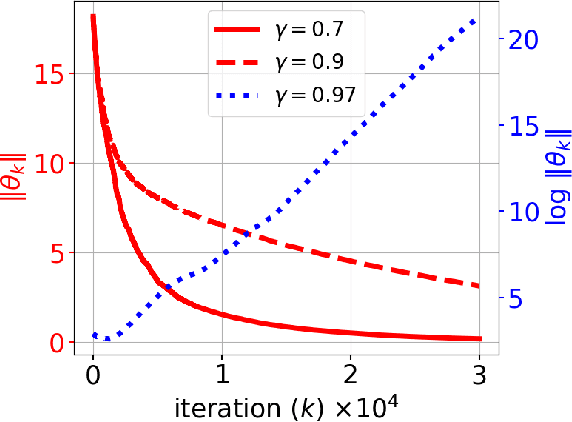
In this paper, we consider the model-free reinforcement learning problem and study the popular Q-learning algorithm with linear function approximation for finding the optimal policy. Despite its popularity, it is known that Q-learning with linear function approximation may diverge in general due to off-policy sampling. Our main contribution is to provide a finite-time bound for the performance of Q-learning with linear function approximation with constant step size under an assumption on the sampling policy. Unlike some prior work in the literature, we do not need to make the unnatural assumption that the samples are i.i.d. (since they are Markovian), and do not require an additional projection step in the algorithm. To show this result, we first consider a more general nonlinear stochastic approximation algorithm with Markovian noise, and derive a finite-time bound on the mean-square error, which we believe is of independent interest. Our proof is based on Lyapunov drift arguments and exploits the geometric mixing of the underlying Markov chain. We also provide numerical simulations to illustrate the effectiveness of our assumption on the sampling policy, and demonstrate the rate of convergence of Q-learning.