ELU-GCN: Effectively Label-Utilizing Graph Convolutional Network

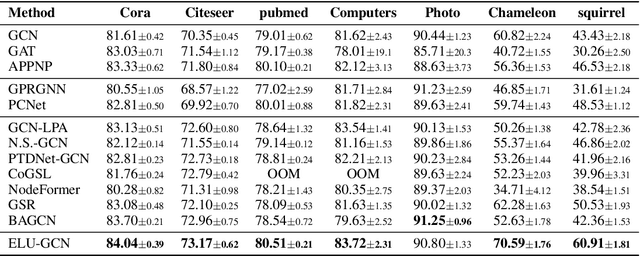
The message-passing mechanism of graph convolutional networks (i.e., GCNs) enables label information to be propagated to a broader range of neighbors, thereby increasing the utilization of labels. However, the label information is not always effectively utilized in the traditional GCN framework. To address this issue, we propose a new two-step framework called ELU-GCN. In the first stage, ELU-GCN conducts graph learning to learn a new graph structure (\ie ELU-graph), which enables GCNs to effectively utilize label information. In the second stage, we design a new graph contrastive learning on the GCN framework for representation learning by exploring the consistency and mutually exclusive information between the learned ELU graph and the original graph. Moreover, we theoretically demonstrate that the proposed method can ensure the generalization ability of GCNs. Extensive experiments validate the superiority of the proposed method.

Building Shortcuts between Distant Nodes with Biaffine Mapping for Graph Convolutional Networks

Multiple recent studies show a paradox in graph convolutional networks (GCNs), that is, shallow architectures limit the capability of learning information from high-order neighbors, while deep architectures suffer from over-smoothing or over-squashing. To enjoy the simplicity of shallow architectures and overcome their limits of neighborhood extension, in this work, we introduce Biaffine technique to improve the expressiveness of graph convolutional networks with a shallow architecture. The core design of our method is to learn direct dependency on long-distance neighbors for nodes, with which only one-hop message passing is capable of capturing rich information for node representation. Besides, we propose a multi-view contrastive learning method to exploit the representations learned from long-distance dependencies. Extensive experiments on nine graph benchmark datasets suggest that the shallow biaffine graph convolutional networks (BAGCN) significantly outperforms state-of-the-art GCNs (with deep or shallow architectures) on semi-supervised node classification. We further verify the effectiveness of biaffine design in node representation learning and the performance consistency on different sizes of training data.

Robust Mid-Pass Filtering Graph Convolutional Networks

Graph convolutional networks (GCNs) are currently the most promising paradigm for dealing with graph-structure data, while recent studies have also shown that GCNs are vulnerable to adversarial attacks. Thus developing GCN models that are robust to such attacks become a hot research topic. However, the structural purification learning-based or robustness constraints-based defense GCN methods are usually designed for specific data or attacks, and introduce additional objective that is not for classification. Extra training overhead is also required in their design. To address these challenges, we conduct in-depth explorations on mid-frequency signals on graphs and propose a simple yet effective Mid-pass filter GCN (Mid-GCN). Theoretical analyses guarantee the robustness of signals through the mid-pass filter, and we also shed light on the properties of different frequency signals under adversarial attacks. Extensive experiments on six benchmark graph data further verify the effectiveness of our designed Mid-GCN in node classification accuracy compared to state-of-the-art GCNs under various adversarial attack strategies.

Learning heterophilious edge to drop: A general framework for boosting graph neural networks

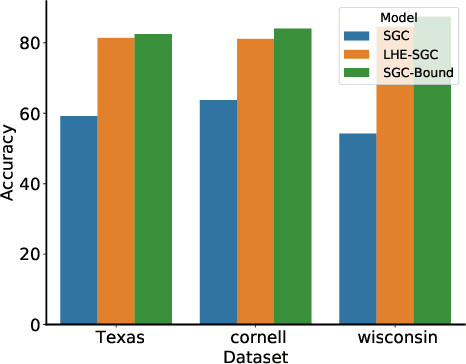
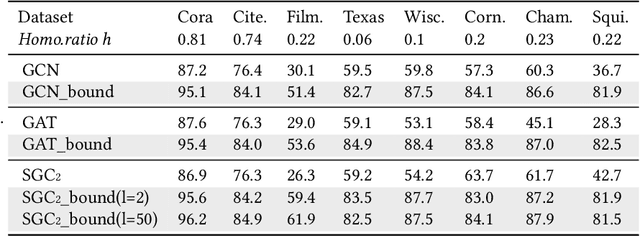
Graph Neural Networks (GNNs) aim at integrating node contents with graph structure to learn nodes/graph representations. Nevertheless, it is found that most of existing GNNs do not work well on data with high heterophily level that accounts for a large proportion of edges between different class labels. Recently, many efforts to tackle this problem focus on optimizing the way of feature learning. From another angle, this work aims at mitigating the negative impacts of heterophily by optimizing graph structure for the first time. Specifically, on assumption that graph smoothing along heterophilious edges can hurt prediction performance, we propose a structure learning method called LHE to identify heterophilious edges to drop. A big advantage of this solution is that it can boost GNNs without careful modification of feature learning strategy. Extensive experiments demonstrate the remarkable performance improvement of GNNs with \emph{LHE} on multiple datasets across full spectrum of homophily level.