Multi-modal Trajectory Prediction for Autonomous Driving with Semantic Map and Dynamic Graph Attention Network

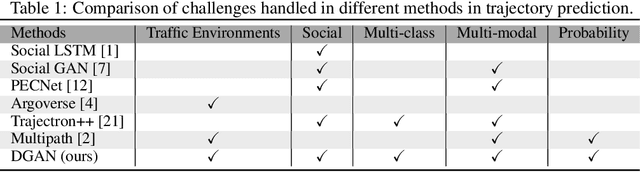
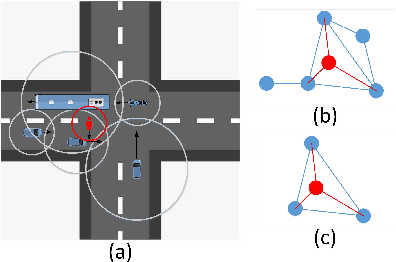
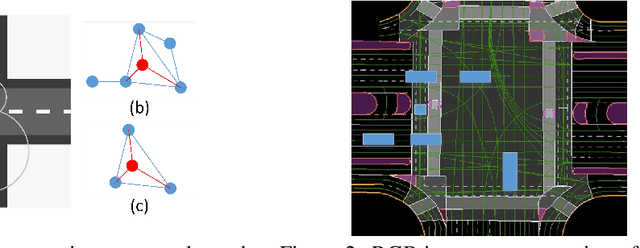
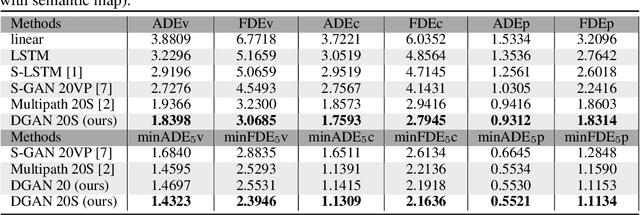
Predicting future trajectories of surrounding obstacles is a crucial task for autonomous driving cars to achieve a high degree of road safety. There are several challenges in trajectory prediction in real-world traffic scenarios, including obeying traffic rules, dealing with social interactions, handling traffic of multi-class movement, and predicting multi-modal trajectories with probability. Inspired by people's natural habit of navigating traffic with attention to their goals and surroundings, this paper presents a unique dynamic graph attention network to solve all those challenges. The network is designed to model the dynamic social interactions among agents and conform to traffic rules with a semantic map. By extending the anchor-based method to multiple types of agents, the proposed method can predict multi-modal trajectories with probabilities for multi-class movements using a single model. We validate our approach on the proprietary autonomous driving dataset for the logistic delivery scenario and two publicly available datasets. The results show that our method outperforms state-of-the-art techniques and demonstrates the potential for trajectory prediction in real-world traffic.

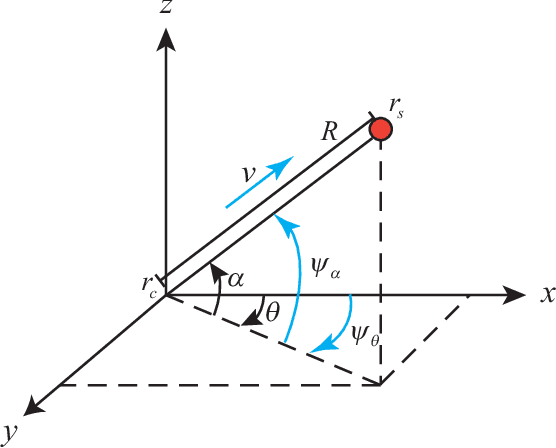
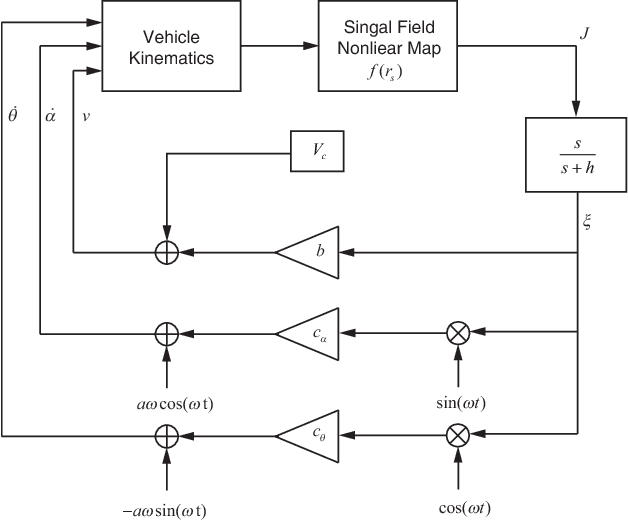
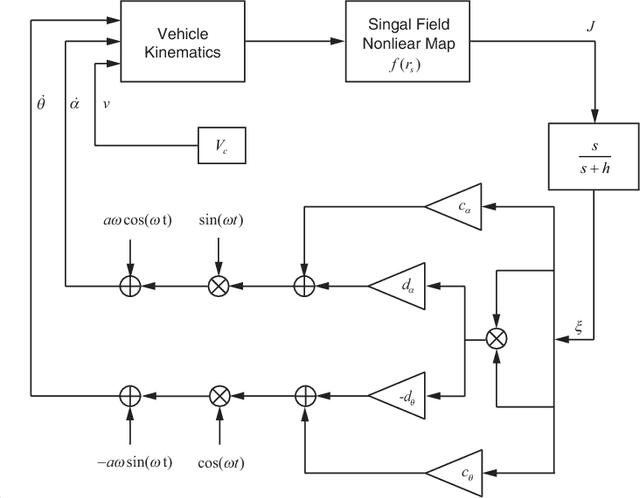
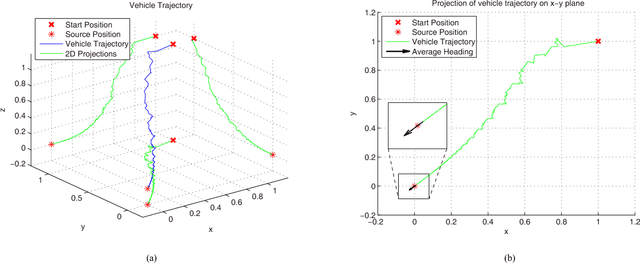
3-D Velocity Regulation for Nonholonomic Source Seeking Without Position Measurement

We consider a three-dimensional problem of steering a nonholonomic vehicle to seek an unknown source of a spatially distributed signal field without any position measurement. In the literature, there exists an extremum seeking-based strategy under a constant forward velocity and tunable pitch and yaw velocities. Obviously, the vehicle with a constant forward velocity may exhibit certain overshoots in the seeking process and can not slow down even it approaches the source. To resolve this undesired behavior, this paper proposes a regulation strategy for the forward velocity along with the pitch and yaw velocities. Under such a strategy, the vehicle slows down near the source and stays within a small area as if it comes to a full stop, and controllers for angular velocities become succinct. We prove the local exponential convergence via the averaging technique. Finally, the theoretical results are illustrated with simulations.