3-D Velocity Regulation for Nonholonomic Source Seeking Without Position Measurement
Paper and Code
Apr 24, 2015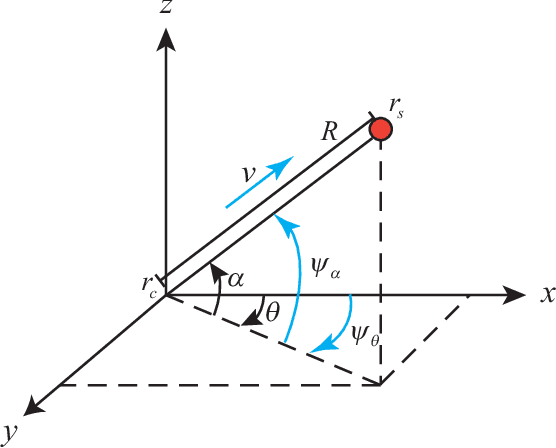
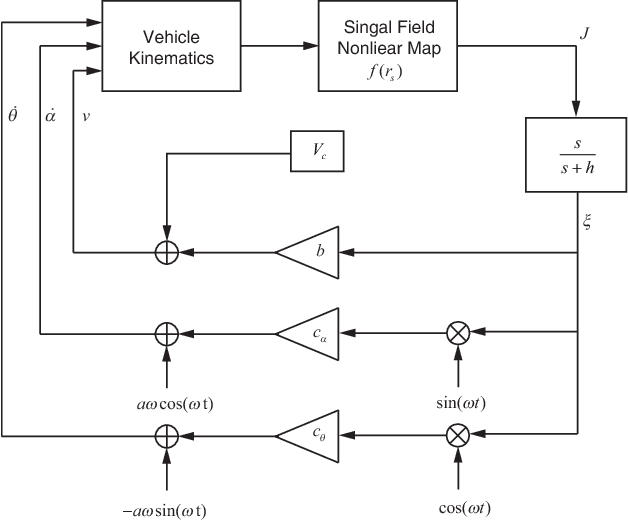
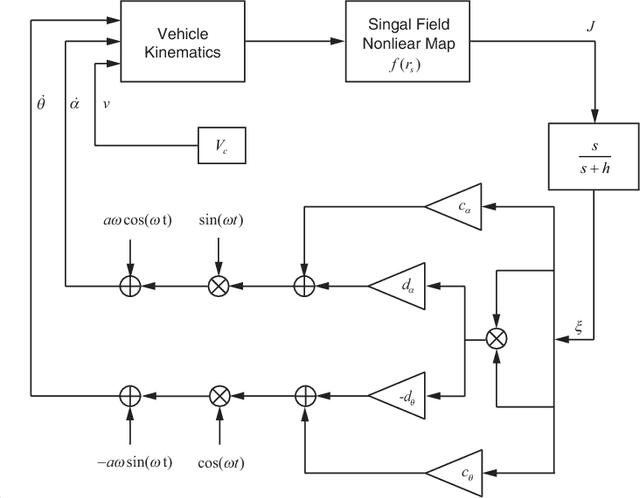
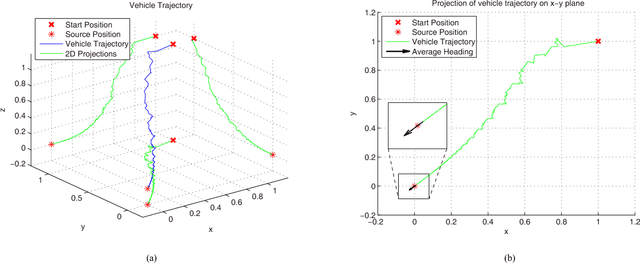
We consider a three-dimensional problem of steering a nonholonomic vehicle to seek an unknown source of a spatially distributed signal field without any position measurement. In the literature, there exists an extremum seeking-based strategy under a constant forward velocity and tunable pitch and yaw velocities. Obviously, the vehicle with a constant forward velocity may exhibit certain overshoots in the seeking process and can not slow down even it approaches the source. To resolve this undesired behavior, this paper proposes a regulation strategy for the forward velocity along with the pitch and yaw velocities. Under such a strategy, the vehicle slows down near the source and stays within a small area as if it comes to a full stop, and controllers for angular velocities become succinct. We prove the local exponential convergence via the averaging technique. Finally, the theoretical results are illustrated with simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge