Jiguo Cao
Online Functional Principal Component Analysis on a Multidimensional Domain
May 04, 2025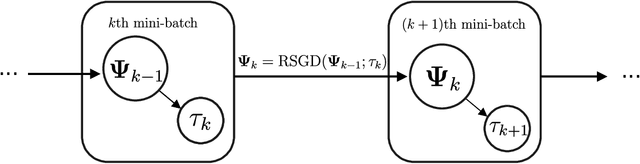
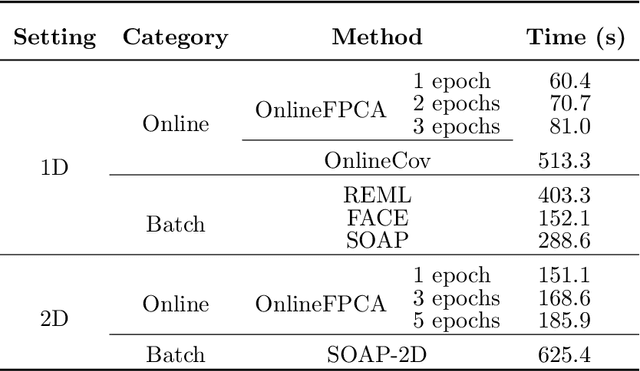
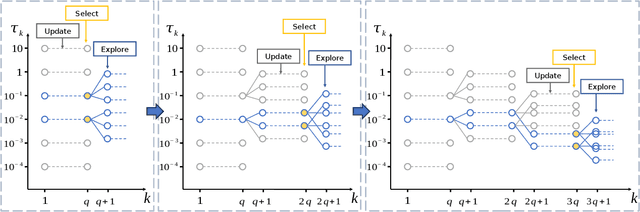
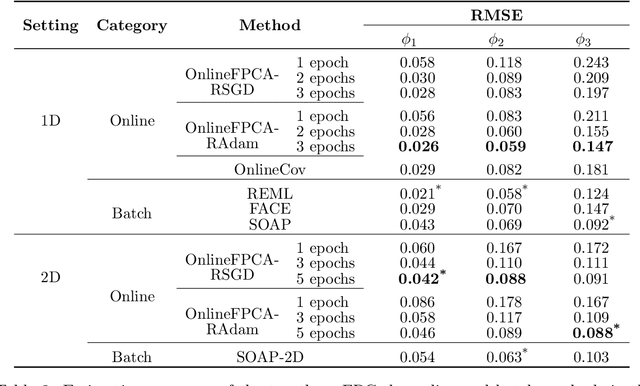
Abstract:Multidimensional functional data streams arise in diverse scientific fields, yet their analysis poses significant challenges. We propose a novel online framework for functional principal component analysis that enables efficient and scalable modeling of such data. Our method represents functional principal components using tensor product splines, enforcing smoothness and orthonormality through a penalized framework on a Stiefel manifold. An efficient Riemannian stochastic gradient descent algorithm is developed, with extensions inspired by adaptive moment estimation and averaging techniques to accelerate convergence. Additionally, a dynamic tuning strategy for smoothing parameter selection is developed based on a rolling averaged block validation score that adapts to the streaming nature of the data. Extensive simulations and real-world applications demonstrate the flexibility and effectiveness of this framework for analyzing multidimensional functional data.
Probabilistic Functional Neural Networks
Mar 27, 2025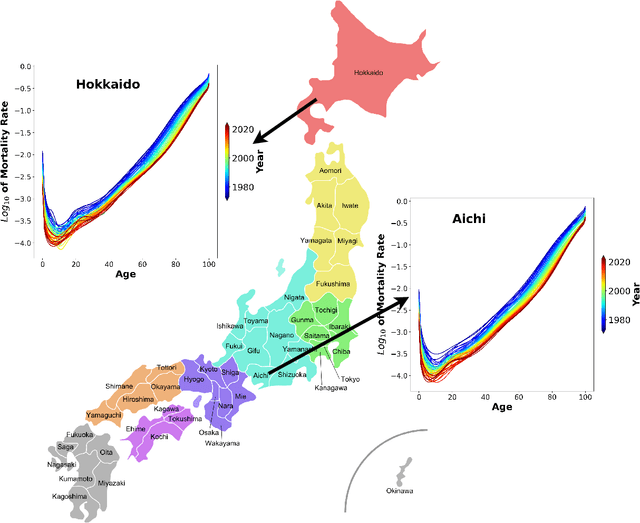
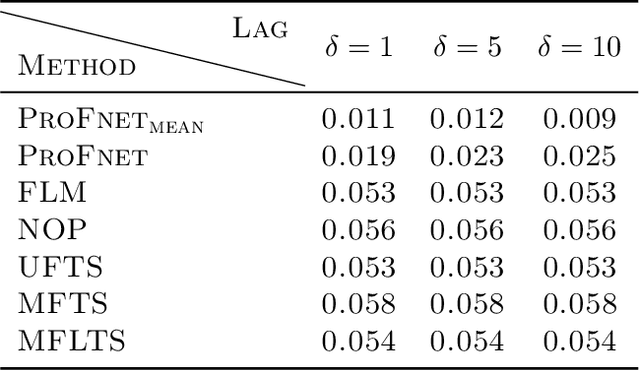
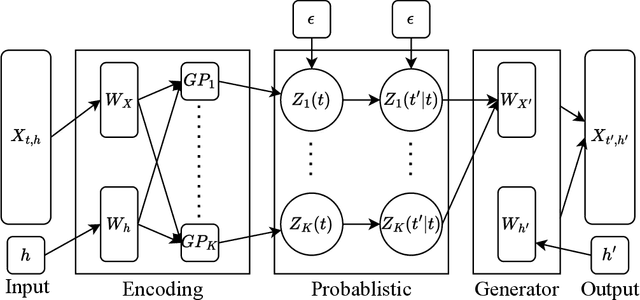
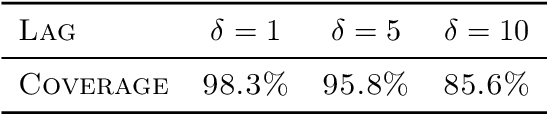
Abstract:High-dimensional functional time series (HDFTS) are often characterized by nonlinear trends and high spatial dimensions. Such data poses unique challenges for modeling and forecasting due to the nonlinearity, nonstationarity, and high dimensionality. We propose a novel probabilistic functional neural network (ProFnet) to address these challenges. ProFnet integrates the strengths of feedforward and deep neural networks with probabilistic modeling. The model generates probabilistic forecasts using Monte Carlo sampling and also enables the quantification of uncertainty in predictions. While capturing both temporal and spatial dependencies across multiple regions, ProFnet offers a scalable and unified solution for large datasets. Applications to Japan's mortality rates demonstrate superior performance. This approach enhances predictive accuracy and provides interpretable uncertainty estimates, making it a valuable tool for forecasting complex high-dimensional functional data and HDFTS.
Representation learning of dynamic networks
Dec 15, 2024Abstract:This study presents a novel representation learning model tailored for dynamic networks, which describes the continuously evolving relationships among individuals within a population. The problem is encapsulated in the dimension reduction topic of functional data analysis. With dynamic networks represented as matrix-valued functions, our objective is to map this functional data into a set of vector-valued functions in a lower-dimensional learning space. This space, defined as a metric functional space, allows for the calculation of norms and inner products. By constructing this learning space, we address (i) attribute learning, (ii) community detection, and (iii) link prediction and recovery of individual nodes in the dynamic network. Our model also accommodates asymmetric low-dimensional representations, enabling the separate study of nodes' regulatory and receiving roles. Crucially, the learning method accounts for the time-dependency of networks, ensuring that representations are continuous over time. The functional learning space we define naturally spans the time frame of the dynamic networks, facilitating both the inference of network links at specific time points and the reconstruction of the entire network structure without direct observation. We validated our approach through simulation studies and real-world applications. In simulations, we compared our methods link prediction performance to existing approaches under various data corruption scenarios. For real-world applications, we examined a dynamic social network replicated across six ant populations, demonstrating that our low-dimensional learning space effectively captures interactions, roles of individual ants, and the social evolution of the network. Our findings align with existing knowledge of ant colony behavior.
Functional Autoencoder for Smoothing and Representation Learning
Jan 17, 2024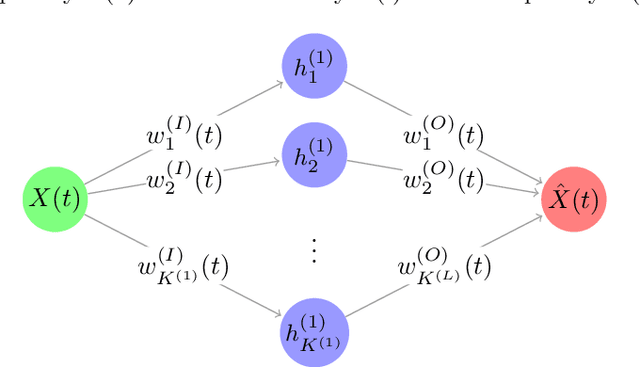
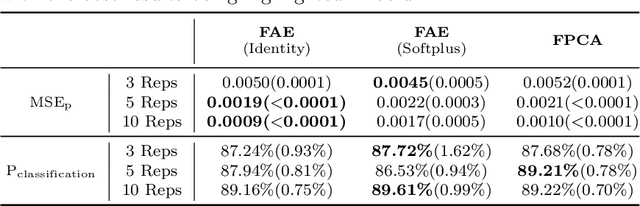
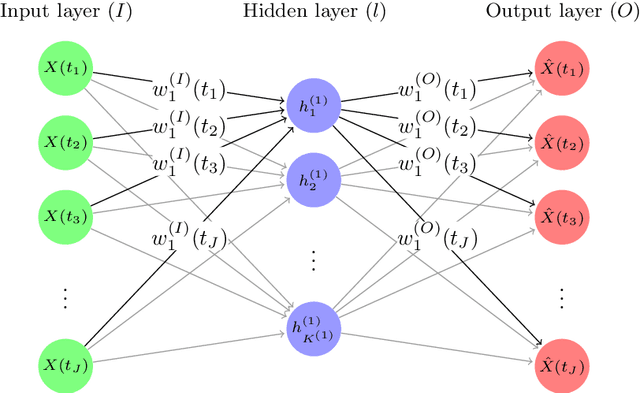
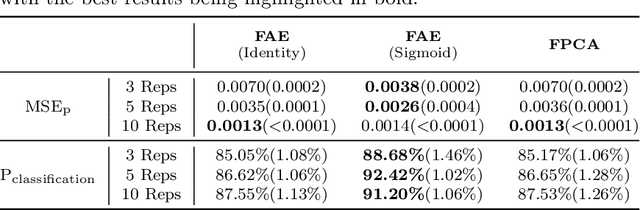
Abstract:A common pipeline in functional data analysis is to first convert the discretely observed data to smooth functions, and then represent the functions by a finite-dimensional vector of coefficients summarizing the information. Existing methods for data smoothing and dimensional reduction mainly focus on learning the linear mappings from the data space to the representation space, however, learning only the linear representations may not be sufficient. In this study, we propose to learn the nonlinear representations of functional data using neural network autoencoders designed to process data in the form it is usually collected without the need of preprocessing. We design the encoder to employ a projection layer computing the weighted inner product of the functional data and functional weights over the observed timestamp, and the decoder to apply a recovery layer that maps the finite-dimensional vector extracted from the functional data back to functional space using a set of predetermined basis functions. The developed architecture can accommodate both regularly and irregularly spaced data. Our experiments demonstrate that the proposed method outperforms functional principal component analysis in terms of prediction and classification, and maintains superior smoothing ability and better computational efficiency in comparison to the conventional autoencoders under both linear and nonlinear settings.
Neural Networks for Scalar Input and Functional Output
Aug 10, 2022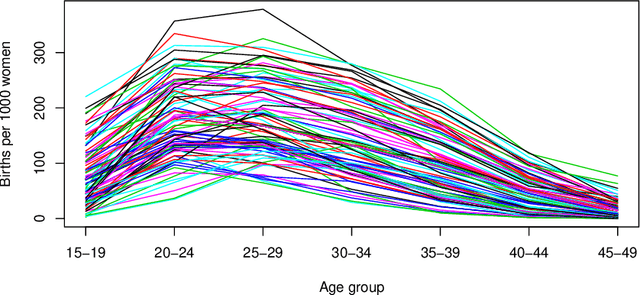
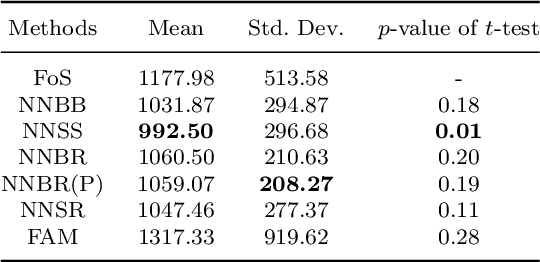
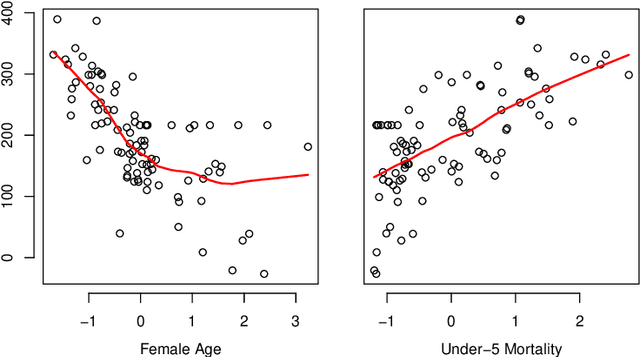
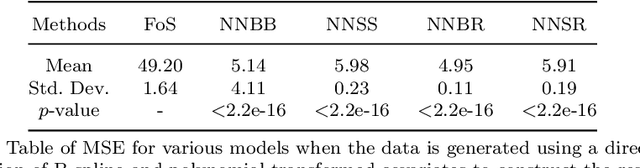
Abstract:The regression of a functional response on a set of scalar predictors can be a challenging task, especially if there is a large number of predictors, these predictors have interaction effects, or the relationship between those predictors and the response is nonlinear. In this work, we propose a solution to this problem: a feed-forward neural network (NN) designed to predict a functional response using scalar inputs. First, we transform the functional response to a finite-dimension representation and then we construct a NN that outputs this representation. We proposed different objective functions to train the NN. The proposed models are suited for both regularly and irregularly spaced data and also provide multiple ways to apply a roughness penalty to control the smoothness of the predicted curve. The difficulty in implementing both those features lies in the definition of objective functions that can be back-propagated. In our experiments, we demonstrate that our model outperforms the conventional function-on-scalar regression model in multiple scenarios while computationally scaling better with the dimension of the predictors.
Functional Nonlinear Learning
Jun 22, 2022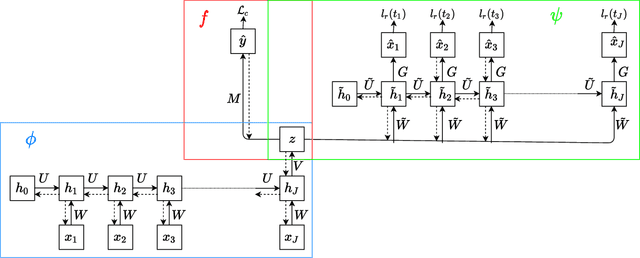

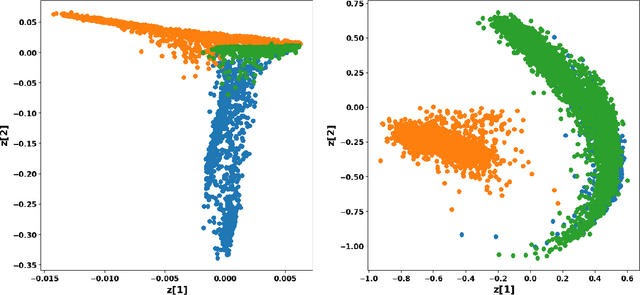
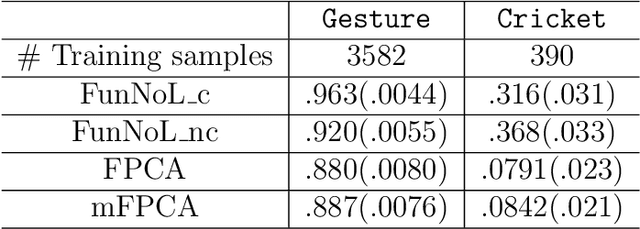
Abstract:Using representations of functional data can be more convenient and beneficial in subsequent statistical models than direct observations. These representations, in a lower-dimensional space, extract and compress information from individual curves. The existing representation learning approaches in functional data analysis usually use linear mapping in parallel to those from multivariate analysis, e.g., functional principal component analysis (FPCA). However, functions, as infinite-dimensional objects, sometimes have nonlinear structures that cannot be uncovered by linear mapping. Linear methods will be more overwhelmed given multivariate functional data. For that matter, this paper proposes a functional nonlinear learning (FunNoL) method to sufficiently represent multivariate functional data in a lower-dimensional feature space. Furthermore, we merge a classification model for enriching the ability of representations in predicting curve labels. Hence, representations from FunNoL can be used for both curve reconstruction and classification. Additionally, we have endowed the proposed model with the ability to address the missing observation problem as well as to further denoise observations. The resulting representations are robust to observations that are locally disturbed by uncontrollable random noises. We apply the proposed FunNoL method to several real data sets and show that FunNoL can achieve better classifications than FPCA, especially in the multivariate functional data setting. Simulation studies have shown that FunNoL provides satisfactory curve classification and reconstruction regardless of data sparsity.
Predicting Time-to-conversion for Dementia of Alzheimer's Type using Multi-modal Deep Survival Analysis
May 02, 2022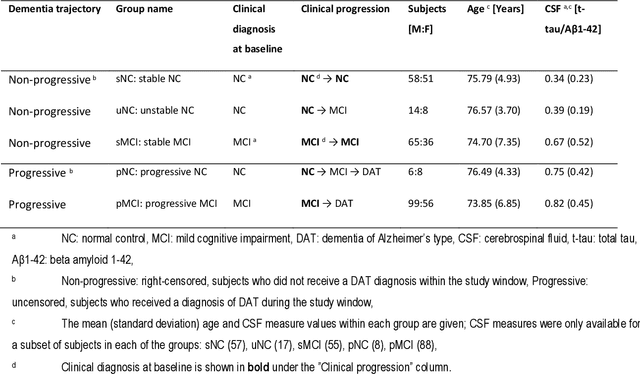
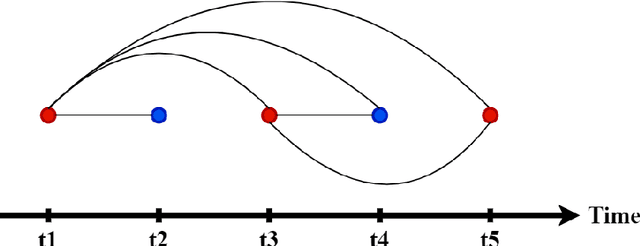

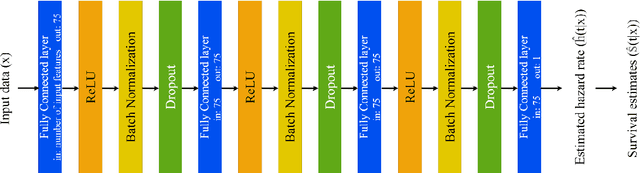
Abstract:Dementia of Alzheimer's Type (DAT) is a complex disorder influenced by numerous factors, but it is unclear how each factor contributes to disease progression. An in-depth examination of these factors may yield an accurate estimate of time-to-conversion to DAT for patients at various disease stages. We used 401 subjects with 63 features from MRI, genetic, and CDC (Cognitive tests, Demographic, and CSF) data modalities in the Alzheimer's Disease Neuroimaging Initiative (ADNI) database. We used a deep learning-based survival analysis model that extends the classic Cox regression model to predict time-to-conversion to DAT. Our findings showed that genetic features contributed the least to survival analysis, while CDC features contributed the most. Combining MRI and genetic features improved survival prediction over using either modality alone, but adding CDC to any combination of features only worked as well as using only CDC features. Consequently, our study demonstrated that using the current clinical procedure, which includes gathering cognitive test results, can outperform survival analysis results produced using costly genetic or CSF data.
Machine Learning Based Multimodal Neuroimaging Genomics Dementia Score for Predicting Future Conversion to Alzheimer's Disease
Mar 11, 2022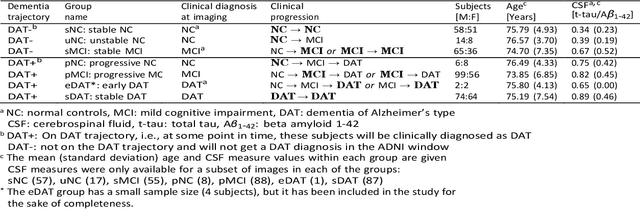
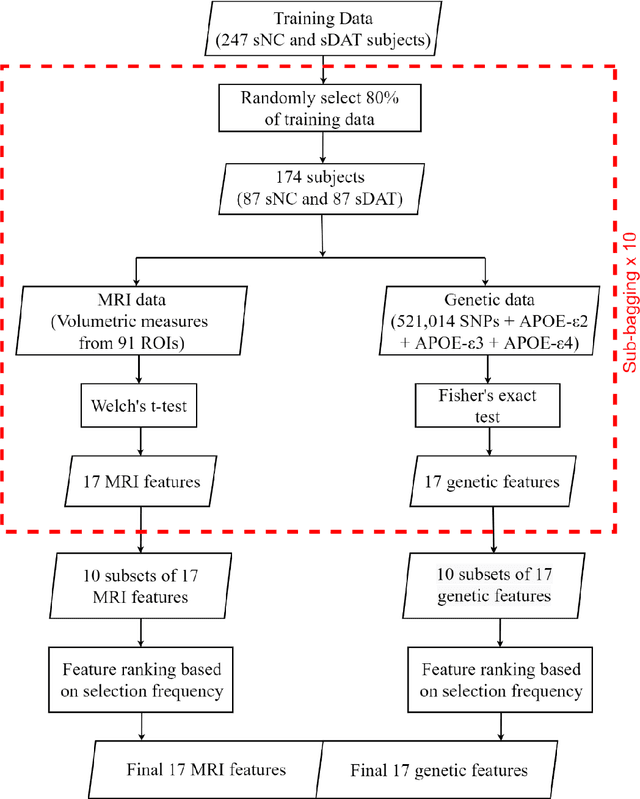

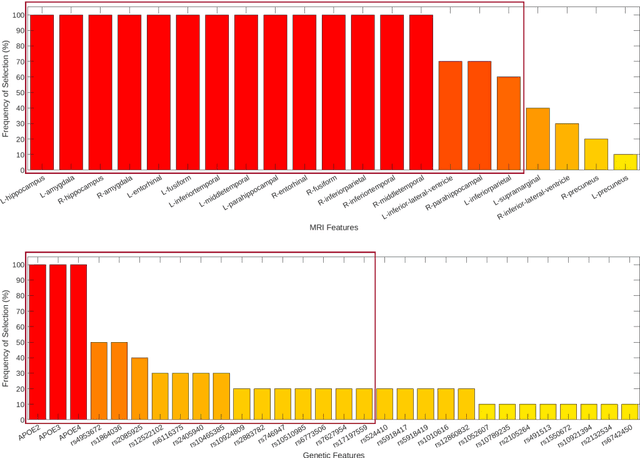
Abstract:Background: The increasing availability of databases containing both magnetic resonance imaging (MRI) and genetic data allows researchers to utilize multimodal data to better understand the characteristics of dementia of Alzheimer's type (DAT). Objective: The goal of this study was to develop and analyze novel biomarkers that can help predict the development and progression of DAT. Methods: We used feature selection and ensemble learning classifier to develop an image/genotype-based DAT score that represents a subject's likelihood of developing DAT in the future. Three feature types were used: MRI only, genetic only, and combined multimodal data. We used a novel data stratification method to better represent different stages of DAT. Using a pre-defined 0.5 threshold on DAT scores, we predicted whether or not a subject would develop DAT in the future. Results: Our results on Alzheimer's Disease Neuroimaging Initiative (ADNI) database showed that dementia scores using genetic data could better predict future DAT progression for currently normal control subjects (Accuracy=0.857) compared to MRI (Accuracy=0.143), while MRI can better characterize subjects with stable mild cognitive impairment (Accuracy=0.614) compared to genetics (Accuracy=0.356). Combining MRI and genetic data showed improved classification performance in the remaining stratified groups. Conclusion: MRI and genetic data can contribute to DAT prediction in different ways. MRI data reflects anatomical changes in the brain, while genetic data can detect the risk of DAT progression prior to the symptomatic onset. Combining information from multimodal data in the right way can improve prediction performance.
Neural Networks as Functional Classifiers
Oct 09, 2020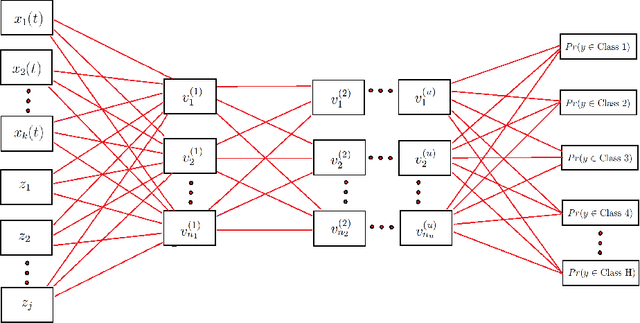
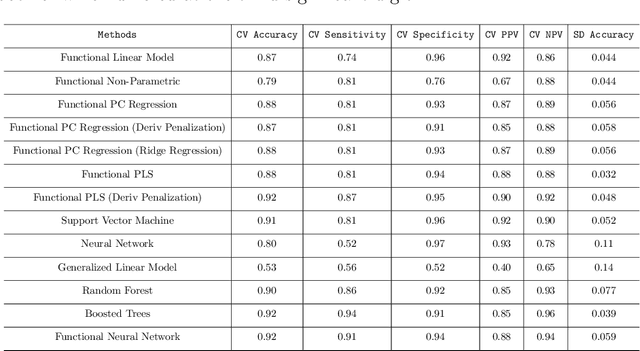
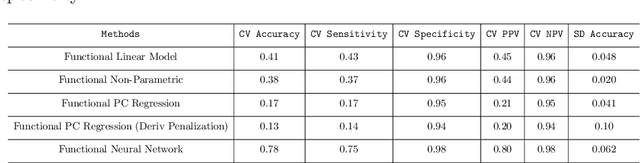
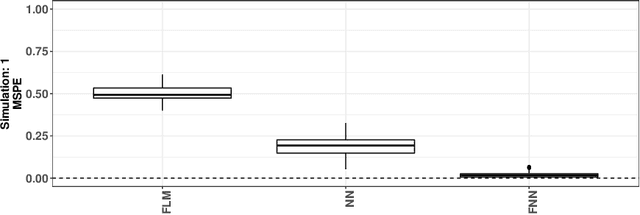
Abstract:In recent years, there has been considerable innovation in the world of predictive methodologies. This is evident by the relative domination of machine learning approaches in various classification competitions. While these algorithms have excelled at multivariate problems, they have remained dormant in the realm of functional data analysis. We extend notable deep learning methodologies to the domain of functional data for the purpose of classification problems. We highlight the effectiveness of our method in a number of classification applications such as classification of spectrographic data. Moreover, we demonstrate the performance of our classifier through simulation studies in which we compare our approach to the functional linear model and other conventional classification methods.
FuncNN: An R Package to Fit Deep Neural Networks Using Generalized Input Spaces
Sep 22, 2020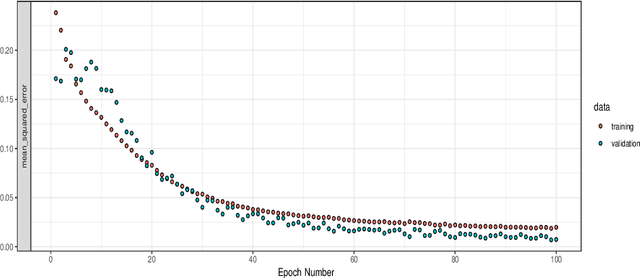
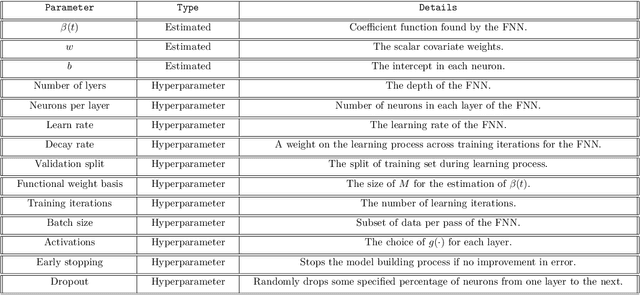
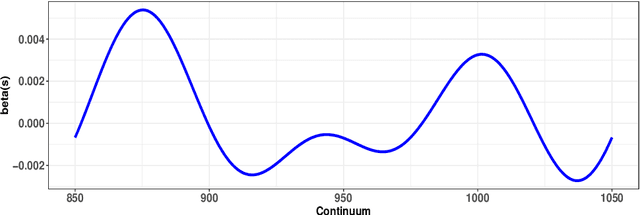

Abstract:Neural networks have excelled at regression and classification problems when the input space consists of scalar variables. As a result of this proficiency, several popular packages have been developed that allow users to easily fit these kinds of models. However, the methodology has excluded the use of functional covariates and to date, there exists no software that allows users to build deep learning models with this generalized input space. To the best of our knowledge, the functional neural network (FuncNN) library is the first such package in any programming language; the library has been developed for R and is built on top of the keras architecture. Throughout this paper, several functions are introduced that provide users an avenue to easily build models, generate predictions, and run cross-validations. A summary of the underlying methodology is also presented. The ultimate contribution is a package that provides a set of general modelling and diagnostic tools for data problems in which there exist both functional and scalar covariates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge