Kevin Multani
Neural Networks as Functional Classifiers
Oct 09, 2020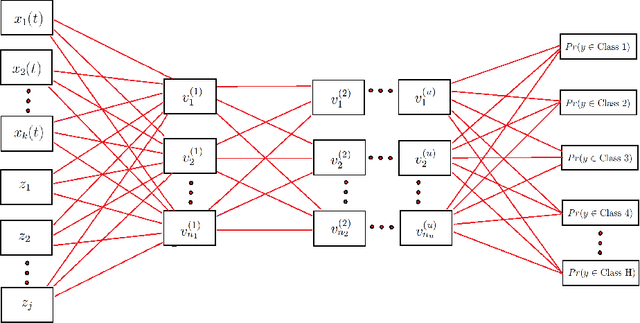
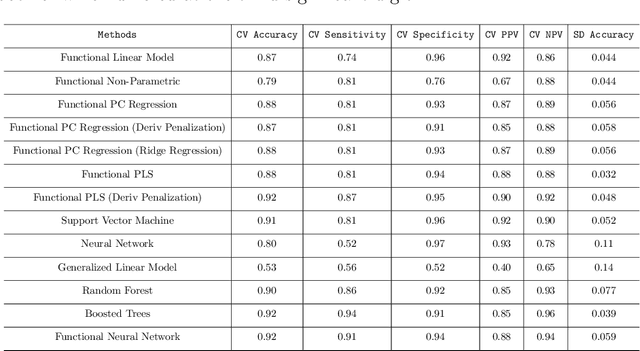
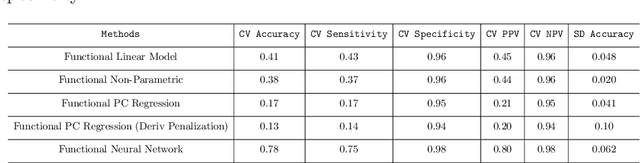
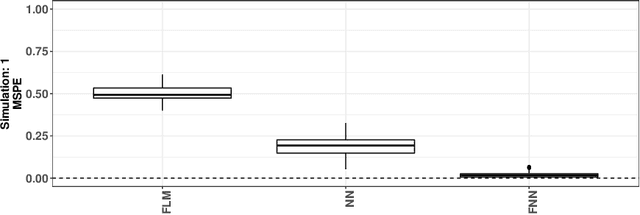
Abstract:In recent years, there has been considerable innovation in the world of predictive methodologies. This is evident by the relative domination of machine learning approaches in various classification competitions. While these algorithms have excelled at multivariate problems, they have remained dormant in the realm of functional data analysis. We extend notable deep learning methodologies to the domain of functional data for the purpose of classification problems. We highlight the effectiveness of our method in a number of classification applications such as classification of spectrographic data. Moreover, we demonstrate the performance of our classifier through simulation studies in which we compare our approach to the functional linear model and other conventional classification methods.
Deep Learning with Functional Inputs
Jun 17, 2020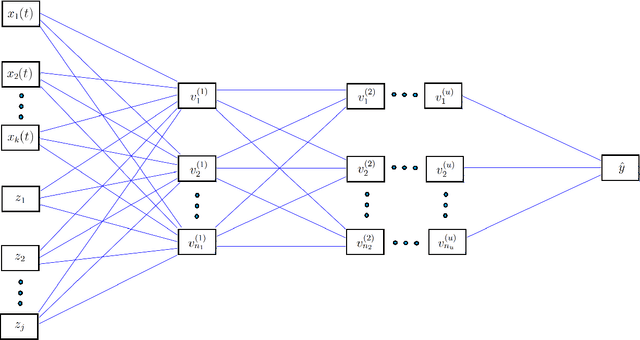
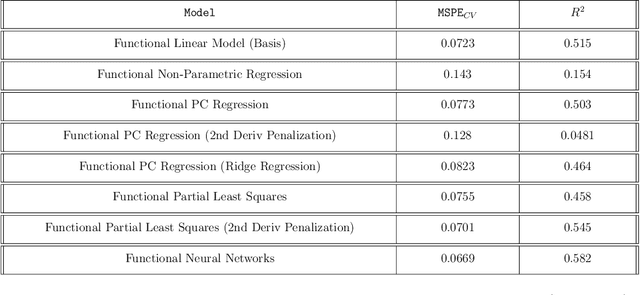
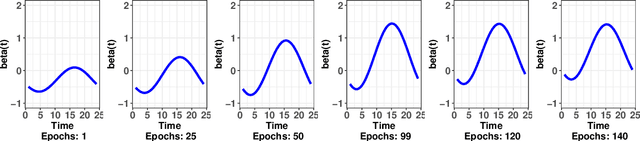
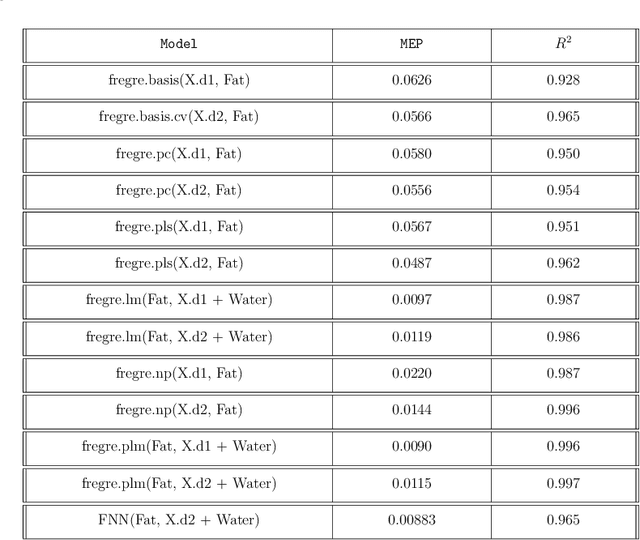
Abstract:We present a methodology for integrating functional data into deep densely connected feed-forward neural networks. The model is defined for scalar responses with multiple functional and scalar covariates. A by-product of the method is a set of dynamic functional weights that can be visualized during the optimization process. This visualization leads to greater interpretability of the relationship between the covariates and the response relative to conventional neural networks. The model is shown to perform well in a number of contexts including prediction of new data and recovery of the true underlying functional weights; these results were confirmed through real applications and simulation studies. A forthcoming R package is developed on top of a popular deep learning library (Keras) allowing for general use of the approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge