Haixu Wang
Probabilistic Functional Neural Networks
Mar 27, 2025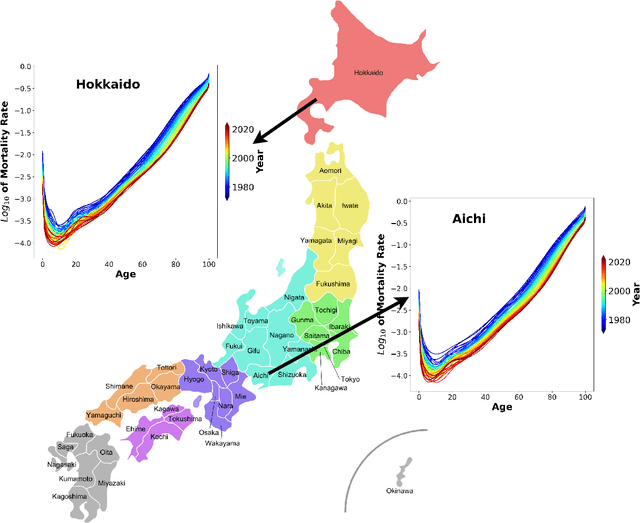
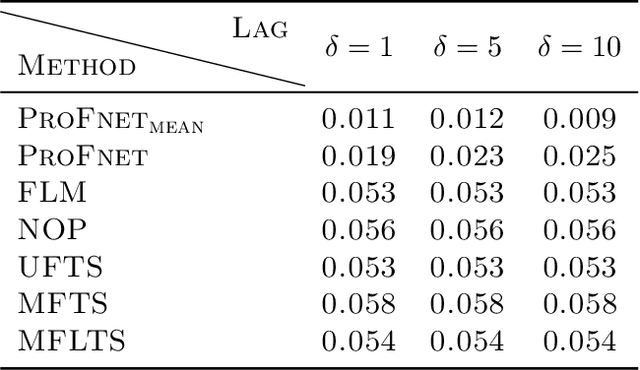
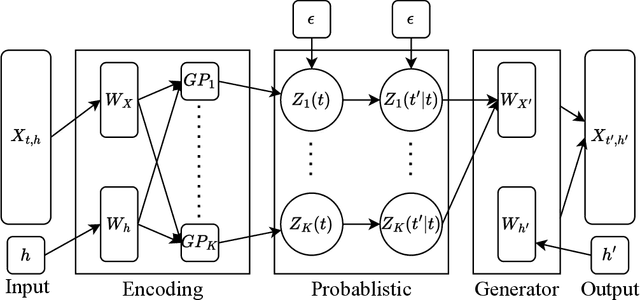
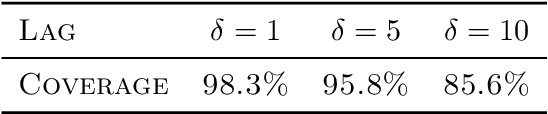
Abstract:High-dimensional functional time series (HDFTS) are often characterized by nonlinear trends and high spatial dimensions. Such data poses unique challenges for modeling and forecasting due to the nonlinearity, nonstationarity, and high dimensionality. We propose a novel probabilistic functional neural network (ProFnet) to address these challenges. ProFnet integrates the strengths of feedforward and deep neural networks with probabilistic modeling. The model generates probabilistic forecasts using Monte Carlo sampling and also enables the quantification of uncertainty in predictions. While capturing both temporal and spatial dependencies across multiple regions, ProFnet offers a scalable and unified solution for large datasets. Applications to Japan's mortality rates demonstrate superior performance. This approach enhances predictive accuracy and provides interpretable uncertainty estimates, making it a valuable tool for forecasting complex high-dimensional functional data and HDFTS.
Representation learning of dynamic networks
Dec 15, 2024Abstract:This study presents a novel representation learning model tailored for dynamic networks, which describes the continuously evolving relationships among individuals within a population. The problem is encapsulated in the dimension reduction topic of functional data analysis. With dynamic networks represented as matrix-valued functions, our objective is to map this functional data into a set of vector-valued functions in a lower-dimensional learning space. This space, defined as a metric functional space, allows for the calculation of norms and inner products. By constructing this learning space, we address (i) attribute learning, (ii) community detection, and (iii) link prediction and recovery of individual nodes in the dynamic network. Our model also accommodates asymmetric low-dimensional representations, enabling the separate study of nodes' regulatory and receiving roles. Crucially, the learning method accounts for the time-dependency of networks, ensuring that representations are continuous over time. The functional learning space we define naturally spans the time frame of the dynamic networks, facilitating both the inference of network links at specific time points and the reconstruction of the entire network structure without direct observation. We validated our approach through simulation studies and real-world applications. In simulations, we compared our methods link prediction performance to existing approaches under various data corruption scenarios. For real-world applications, we examined a dynamic social network replicated across six ant populations, demonstrating that our low-dimensional learning space effectively captures interactions, roles of individual ants, and the social evolution of the network. Our findings align with existing knowledge of ant colony behavior.
Functional Nonlinear Learning
Jun 22, 2022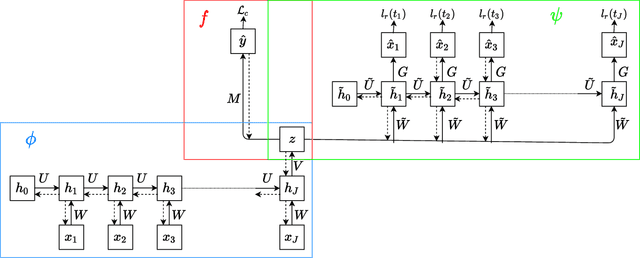

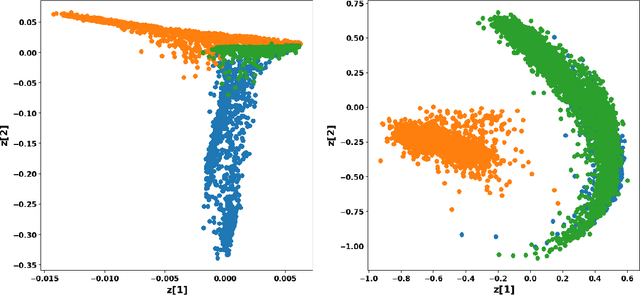
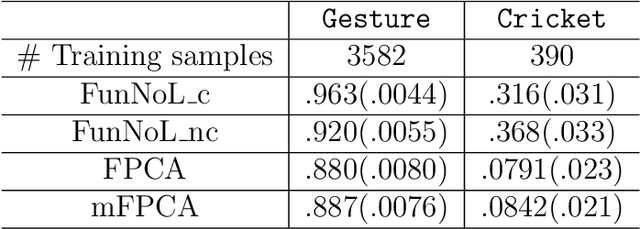
Abstract:Using representations of functional data can be more convenient and beneficial in subsequent statistical models than direct observations. These representations, in a lower-dimensional space, extract and compress information from individual curves. The existing representation learning approaches in functional data analysis usually use linear mapping in parallel to those from multivariate analysis, e.g., functional principal component analysis (FPCA). However, functions, as infinite-dimensional objects, sometimes have nonlinear structures that cannot be uncovered by linear mapping. Linear methods will be more overwhelmed given multivariate functional data. For that matter, this paper proposes a functional nonlinear learning (FunNoL) method to sufficiently represent multivariate functional data in a lower-dimensional feature space. Furthermore, we merge a classification model for enriching the ability of representations in predicting curve labels. Hence, representations from FunNoL can be used for both curve reconstruction and classification. Additionally, we have endowed the proposed model with the ability to address the missing observation problem as well as to further denoise observations. The resulting representations are robust to observations that are locally disturbed by uncontrollable random noises. We apply the proposed FunNoL method to several real data sets and show that FunNoL can achieve better classifications than FPCA, especially in the multivariate functional data setting. Simulation studies have shown that FunNoL provides satisfactory curve classification and reconstruction regardless of data sparsity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge