Computing a Task-Dependent Grasp Metric Using Second Order Cone Programs

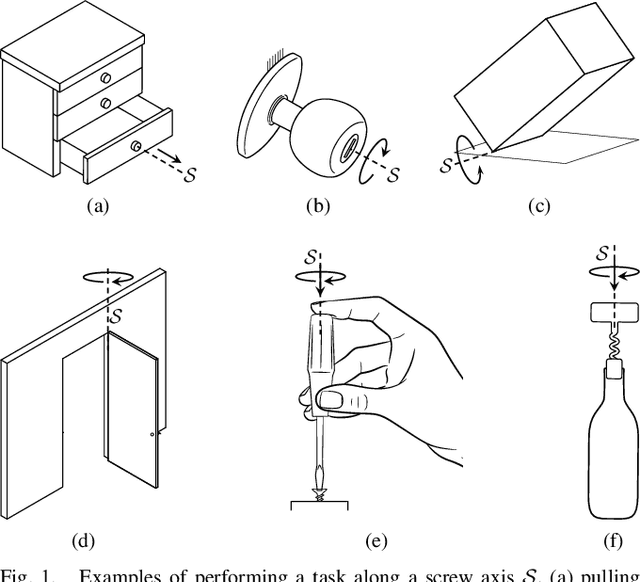
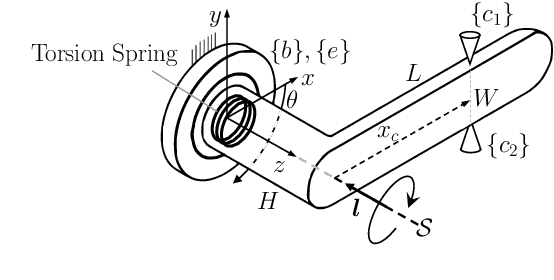
Evaluating a grasp generated by a set of hand-object contact locations is a key component of many grasp planning algorithms. In this paper, we present a novel second order cone program (SOCP) based optimization formulation for evaluating a grasps' ability to apply wrenches to generate a linear motion along a given direction and/or an angular motion about the given direction. Our quality measure can be computed efficiently, since the SOCP is a convex optimization problem, which can be solved optimally with interior point methods. A key feature of our approach is that we can consider the effect of contact wrenches from any contact of the object with the environment. This is different from the extant literature where only the effect of finger-object contacts is considered. Exploiting the environmental contact is useful in many manipulation scenarios either to enhance the dexterity of simple hands or improve the payload capability of the manipulator. In contrast to most existing approaches, our approach also takes into account the practical constraint that the maximum contact force that can be applied at a finger-object contact can be different for each contact. We can also include the effect of external forces like gravity, as well as the joint torque constraints of the fingers/manipulators. Furthermore, for a given motion path as a constant screw motion or a sequence of constant screw motions, we can discretize the path and compute a global grasp metric to accomplish the whole task with a chosen set of finger-object contact locations.

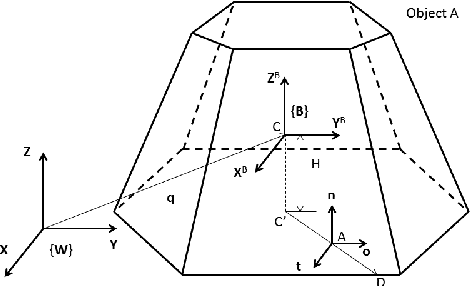
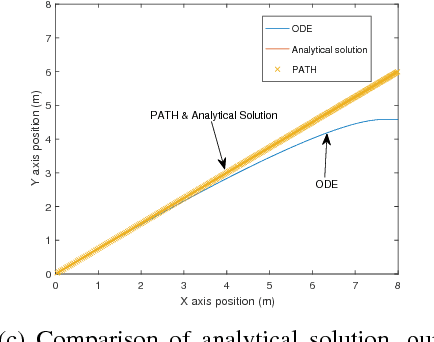
Rigid Body Dynamic Simulation with Line and Surface Contact

In this paper, we develop a principled method to model line and surface contact with point contact (we call this point, equivalent contact point) that is consistent with physics-based models of surface (line) contact. Assuming that the set of contact points form a convex set, we solve the contact detection and dynamic simulation step simultaneously by formulating the problem as a mixed nonlinear complementarity problem. This allows us to simultaneously compute the equivalent contact point as well as the wrenches (forces and moments) at the equivalent contact point (consistent with the friction model) along with the configuration and velocities of the rigid objects. Furthermore, we prove that the contact constraints of no inter-penetration between the objects is also satisfied. We present a geometrically implicit time-stepping scheme for dynamic simulation for contacts between two bodies with convex contact area, which includes line contact and surface contact. We prove that for surface and line contact, for any value of the velocity of center of mass of the object, there is a unique solution for contact point and contact wrench that satisfies the discrete-time equations of motion. Simulation examples are shown to demonstrate the validity of our approach and show that with our approach we can seamlessly transition between point, line, and surface contact.

Dynamic Simulation-Guided Design of Tumbling Magnetic Microrobots

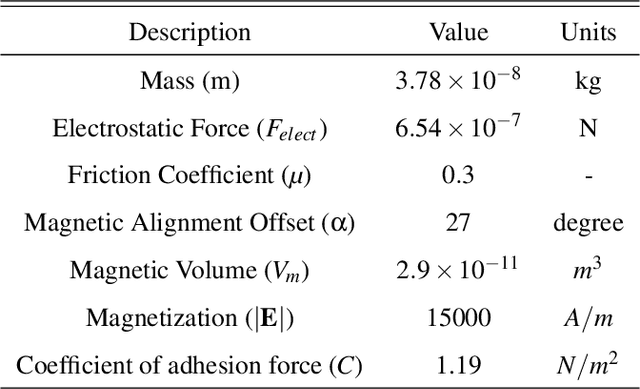
Design of robots at the small scale is a trial-and-error based process, which is costly and time-consuming. There are few dynamic simulation tools available to accurately predict the motion or performance of untethered microrobots as they move over a substrate. At smaller length scales, the influence of adhesion and friction, which scales with surface area, becomes more pronounced. Thus, rigid body dynamic simulators, which implicitly assume that contact between two bodies can be modeled as point contact are not suitable. In this paper, we present techniques for simulating the motion of microrobots where there can be intermittent and non-point contact between the robot and the substrate. We use these techniques to study the motion of tumbling microrobots of different shapes and select shapes that are optimal for improving locomotion performance. Simulation results are verified using experimental data on linear velocity, maximum climbable incline angle, and microrobot trajectory. Microrobots with improved geometry were fabricated, but limitations in the fabrication process resulted in unexpected manufacturing errors and material/size scale adjustments. The developed simulation model is able to incorporate these limitations and emulate their effect on the microrobot's motion, reproducing the experimental behavior of the tumbling microrobots, further showcasing the effectiveness of having such a dynamic model.

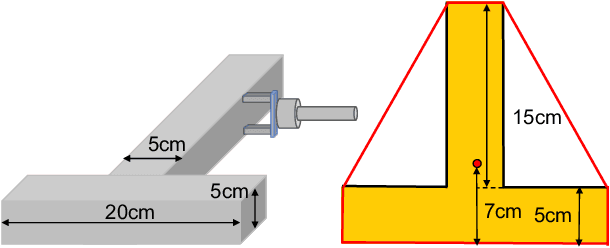
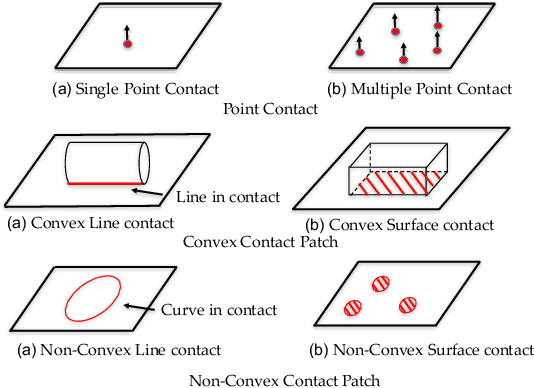
Modeling and Prediction of Rigid Body Motion with Planar Non-Convex Contact

We present a principled method for motion prediction via dynamic simulation for rigid bodies in intermittent contact with each other where the contact region is a planar non-convex contact patch. Such methods are useful in planning and control for robotic manipulation. The planar non-convex contact patch can either be a topologically connected set or disconnected set. Most work in rigid body dynamic simulation assume that the contact between objects is a point contact, which may not be valid in many applications. In this paper, by using the convex hull of the contact patch, we build on our recent work on simulating rigid bodies with convex contact patches for simulating motion of objects with planar non-convex contact patches. We formulate a discrete-time mixed complementarity problem where we solve the contact detection and integration of the equations of motion simultaneously. We solve for the equivalent contact point (ECP) and contact impulse of each contact patch simultaneously along with the state, i.e., configuration and velocity of the objects. We prove that although we are representing a patch contact by an equivalent point, our model for enforcing non-penetration constraints ensure that there is no artificial penetration between the contacting rigid bodies. We provide empirical evidence to show that our method can seamlessly capture transition among different contact modes like patch contact, multiple or single point contact.

Towards Dynamic Simulation Guided Optimal Design of Tumbling Microrobots

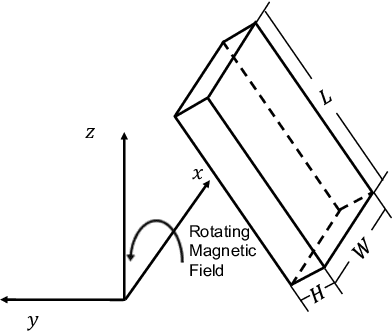
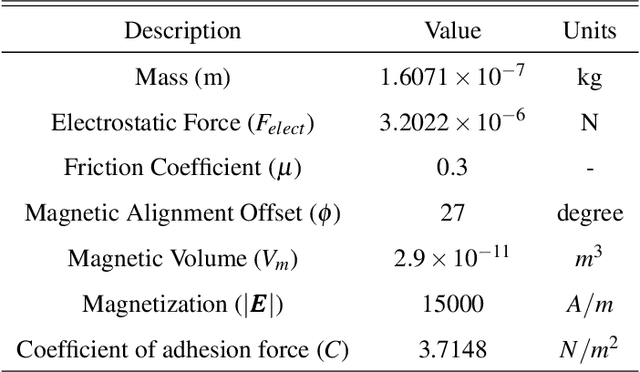
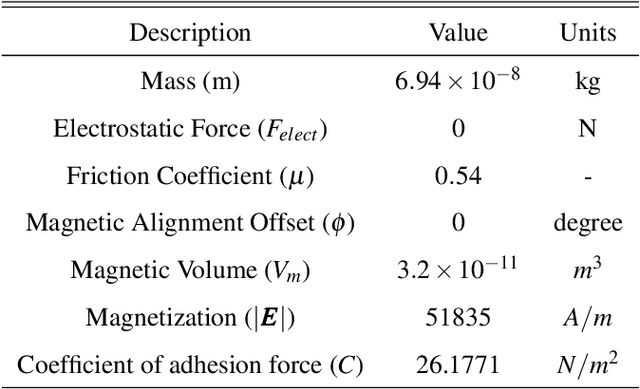
Design of robots at the small scale is a trial-and-error based process, which is costly and time-consuming. There are no good dynamic simulation tools to predict the motion or performance of a microrobot as it moves against a substrate. At smaller length scales, the influence of adhesion and friction, which scales with surface area, becomes more pronounced. Thus, rigid body dynamic simulators, which implicitly assume that contact between two bodies can be modeled as point contact are not suitable. In this paper, we present techniques for simulating the motion of microrobots where there can be intermittent and non-point contact between the robot and the substrate. We use this simulator to study the motion of microrobots of different shapes and select shapes that are most promising for performing a given task.

Rigid Body Motion Prediction with Planar Non-convex Contact Patch

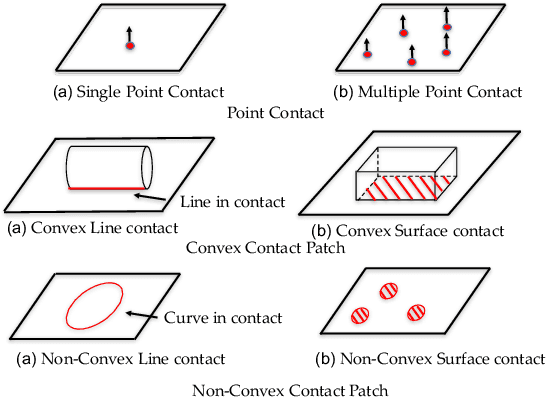
We present a principled method for motion prediction via dynamic simulation for rigid bodies in intermittent contact with each other where the contact is assumed to be a planar non-convex contact patch. The planar non-convex contact patch can either be a topologically connected set or disconnected set. Such algorithms are useful in planning and control for robotic manipulation. Most works in rigid body dynamic simulation assume that the contact between objects is a point contact, which may not be valid in many applications. In this paper, by using the convex hull of the contact patch, we build on our recent work on simulating rigid bodies with convex contact patches, for simulating the motion of objects with planar non-convex contact patches. We formulate a discrete-time mixed complementarity problem where we solve the contact detection and integration of the equations of motion simultaneously. Thus, our method is a geometrically-implicit method and we prove that in our formulation, there is no artificial penetration between the contacting rigid bodies. We solve for the equivalent contact point (ECP) and contact impulse of each contact patch simultaneously along with the state, i.e., configuration and velocity of the objects. We provide empirical evidence to show that our method can seamlessly capture the transition between different contact modes like patch contact to multiple or single point contact during the simulation.

Dynamic Model of Planar Sliding

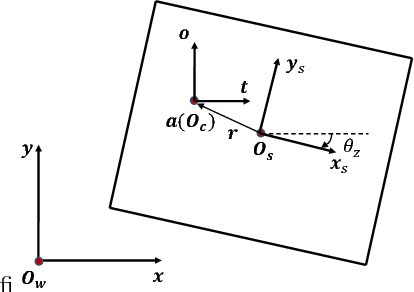
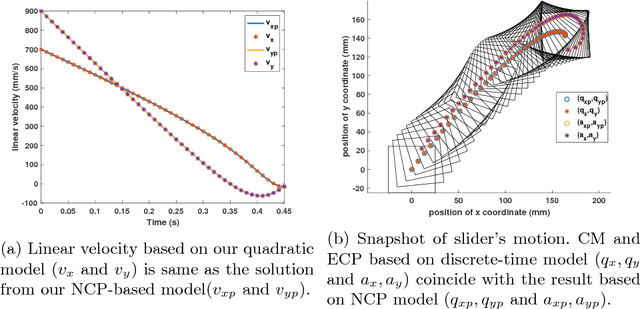
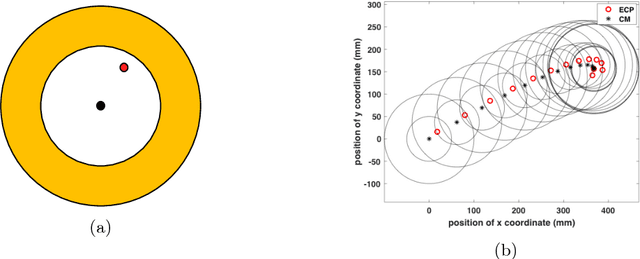
In this paper, we present a principled method to model general planar sliding motion with distributed convex contact patch. The effect of contact patch with indeterminate pressure distribution can be equivalently modeled as the contact wrench at one point contact. We call this point equivalent contact point. Our dynamic model embeds ECP within the equations of slider's motion and friction model which approximates the distributed contact patch, and eventually brings us a system of quadratic equations. This discrete-time dynamic model allows us to solve for the two components of tangential friction impulses, the friction moment and the slip speed. The state of the slider as well as the ECP can be computed by solving a system of linear equations once the contact impulses are computed. In addition, we derive the closed form solutions for the state of slider for quasi-static motion. Furthermore, in pure translation case, based on the discrete-time model, we present the closed form expressions for the friction impulses the slider suffers and the state of it at each time step. Simulation examples are shown to demonstrate the validity of our approach.

Rigid Body Dynamic Simulation with Multiple Convex Contact Patches

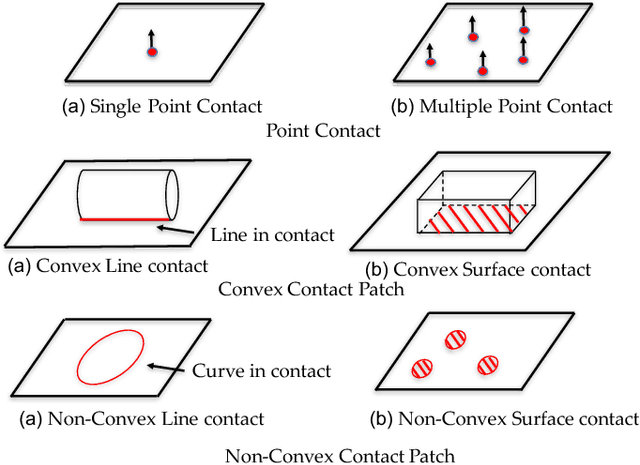
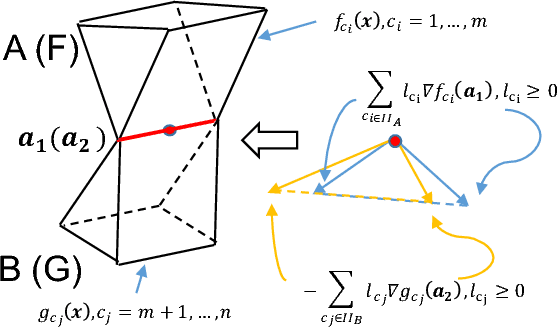
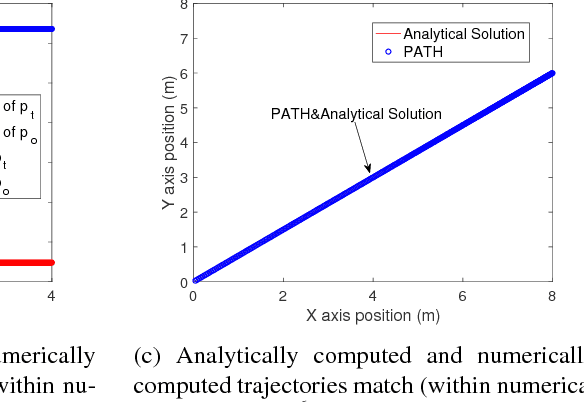
We present a principled method for dynamic simulation of rigid bodies in intermittent contact with each other where the contact is assumed to be a non-convex contact patch that can be modeled as a union of convex patches. The prevalent assumption in simulating rigid bodies undergoing intermittent contact with each other is that the contact is a point contact. In recent work, we introduced an approach to simulate contacting rigid bodies with convex contact patches (line and surface contact). In this paper, for non-convex contact patches modeled as a union of convex patches, we formulate a discrete-time mixed complementarity problem where we solve the contact detection and integration of the equations of motion simultaneously. Thus, our method is a geometrically-implicit method and we prove that in our formulation, there is no artificial penetration between the contacting rigid bodies. We solve for the equivalent contact point (ECP) and contact impulse of each contact patch simultaneously along with the state, i.e., configuration and velocity of the objects. We provide empirical evidence to show that if the number of contact patches between two objects is less than or equal to three, the state evolution of the bodies is unique, although the contact impulses and ECP may not be unique. We also present simulation results showing that our method can seamlessly capture transition between different contact modes like non-convex patch to point (or line contact) and vice-versa during simulation.