Rigid Body Motion Prediction with Planar Non-convex Contact Patch
Paper and Code
Apr 15, 2019
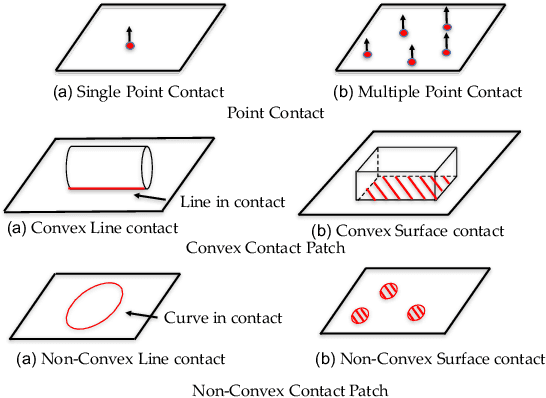


We present a principled method for motion prediction via dynamic simulation for rigid bodies in intermittent contact with each other where the contact is assumed to be a planar non-convex contact patch. The planar non-convex contact patch can either be a topologically connected set or disconnected set. Such algorithms are useful in planning and control for robotic manipulation. Most works in rigid body dynamic simulation assume that the contact between objects is a point contact, which may not be valid in many applications. In this paper, by using the convex hull of the contact patch, we build on our recent work on simulating rigid bodies with convex contact patches, for simulating the motion of objects with planar non-convex contact patches. We formulate a discrete-time mixed complementarity problem where we solve the contact detection and integration of the equations of motion simultaneously. Thus, our method is a geometrically-implicit method and we prove that in our formulation, there is no artificial penetration between the contacting rigid bodies. We solve for the equivalent contact point (ECP) and contact impulse of each contact patch simultaneously along with the state, i.e., configuration and velocity of the objects. We provide empirical evidence to show that our method can seamlessly capture the transition between different contact modes like patch contact to multiple or single point contact during the simulation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge