Dynamic Model of Planar Sliding
Paper and Code
Jan 14, 2019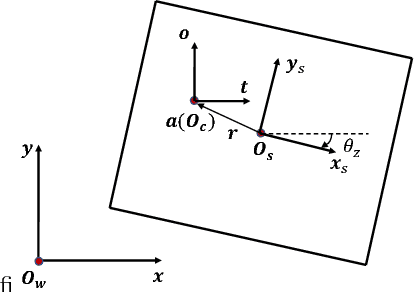

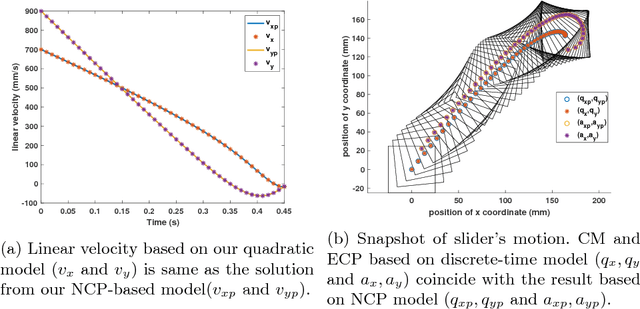
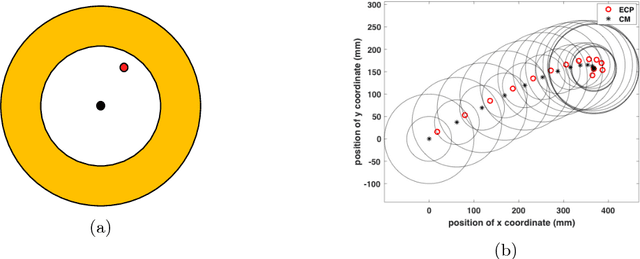
In this paper, we present a principled method to model general planar sliding motion with distributed convex contact patch. The effect of contact patch with indeterminate pressure distribution can be equivalently modeled as the contact wrench at one point contact. We call this point equivalent contact point. Our dynamic model embeds ECP within the equations of slider's motion and friction model which approximates the distributed contact patch, and eventually brings us a system of quadratic equations. This discrete-time dynamic model allows us to solve for the two components of tangential friction impulses, the friction moment and the slip speed. The state of the slider as well as the ECP can be computed by solving a system of linear equations once the contact impulses are computed. In addition, we derive the closed form solutions for the state of slider for quasi-static motion. Furthermore, in pure translation case, based on the discrete-time model, we present the closed form expressions for the friction impulses the slider suffers and the state of it at each time step. Simulation examples are shown to demonstrate the validity of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge