Rigid Body Dynamic Simulation with Multiple Convex Contact Patches
Paper and Code
Sep 14, 2018
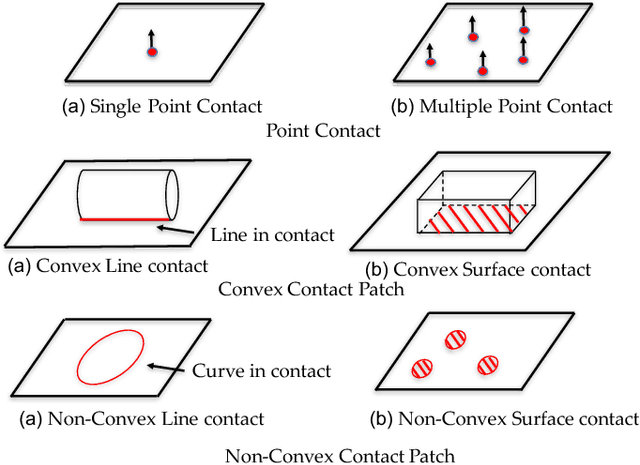
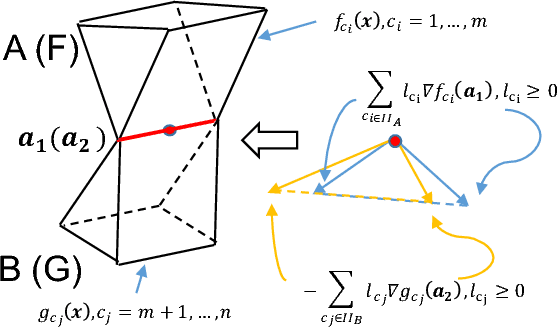
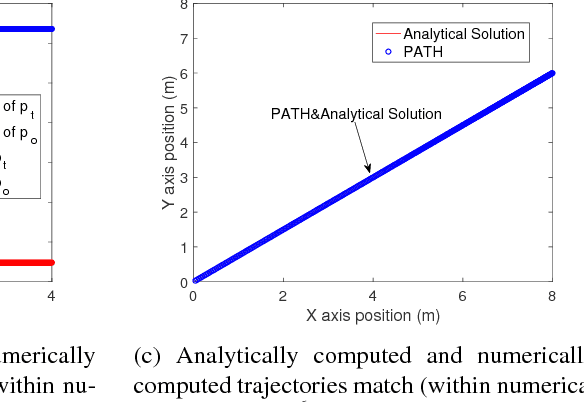
We present a principled method for dynamic simulation of rigid bodies in intermittent contact with each other where the contact is assumed to be a non-convex contact patch that can be modeled as a union of convex patches. The prevalent assumption in simulating rigid bodies undergoing intermittent contact with each other is that the contact is a point contact. In recent work, we introduced an approach to simulate contacting rigid bodies with convex contact patches (line and surface contact). In this paper, for non-convex contact patches modeled as a union of convex patches, we formulate a discrete-time mixed complementarity problem where we solve the contact detection and integration of the equations of motion simultaneously. Thus, our method is a geometrically-implicit method and we prove that in our formulation, there is no artificial penetration between the contacting rigid bodies. We solve for the equivalent contact point (ECP) and contact impulse of each contact patch simultaneously along with the state, i.e., configuration and velocity of the objects. We provide empirical evidence to show that if the number of contact patches between two objects is less than or equal to three, the state evolution of the bodies is unique, although the contact impulses and ECP may not be unique. We also present simulation results showing that our method can seamlessly capture transition between different contact modes like non-convex patch to point (or line contact) and vice-versa during simulation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge