Rigid Body Dynamic Simulation with Line and Surface Contact
Paper and Code
Oct 07, 2020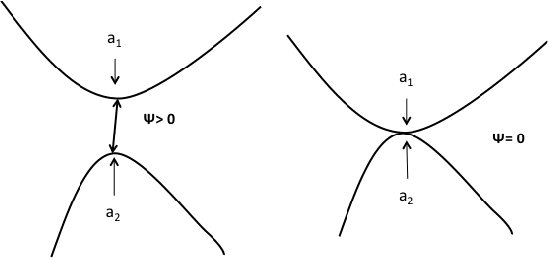
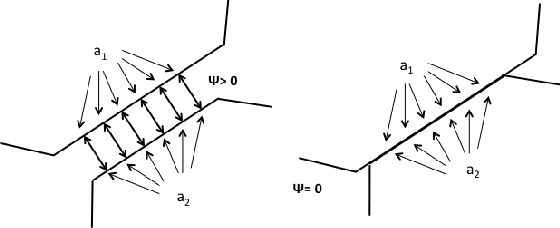
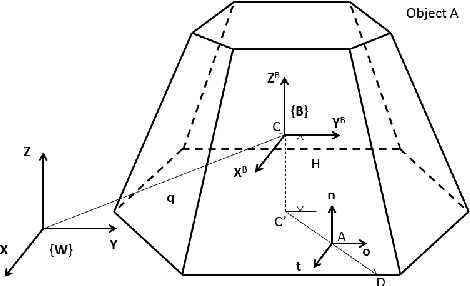
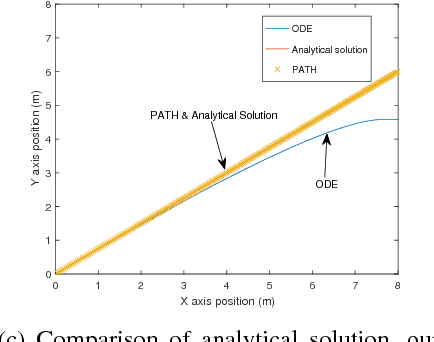
In this paper, we develop a principled method to model line and surface contact with point contact (we call this point, equivalent contact point) that is consistent with physics-based models of surface (line) contact. Assuming that the set of contact points form a convex set, we solve the contact detection and dynamic simulation step simultaneously by formulating the problem as a mixed nonlinear complementarity problem. This allows us to simultaneously compute the equivalent contact point as well as the wrenches (forces and moments) at the equivalent contact point (consistent with the friction model) along with the configuration and velocities of the rigid objects. Furthermore, we prove that the contact constraints of no inter-penetration between the objects is also satisfied. We present a geometrically implicit time-stepping scheme for dynamic simulation for contacts between two bodies with convex contact area, which includes line contact and surface contact. We prove that for surface and line contact, for any value of the velocity of center of mass of the object, there is a unique solution for contact point and contact wrench that satisfies the discrete-time equations of motion. Simulation examples are shown to demonstrate the validity of our approach and show that with our approach we can seamlessly transition between point, line, and surface contact.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge