PixelMan: Consistent Object Editing with Diffusion Models via Pixel Manipulation and Generation

Recent research explores the potential of Diffusion Models (DMs) for consistent object editing, which aims to modify object position, size, and composition, etc., while preserving the consistency of objects and background without changing their texture and attributes. Current inference-time methods often rely on DDIM inversion, which inherently compromises efficiency and the achievable consistency of edited images. Recent methods also utilize energy guidance which iteratively updates the predicted noise and can drive the latents away from the original image, resulting in distortions. In this paper, we propose PixelMan, an inversion-free and training-free method for achieving consistent object editing via Pixel Manipulation and generation, where we directly create a duplicate copy of the source object at target location in the pixel space, and introduce an efficient sampling approach to iteratively harmonize the manipulated object into the target location and inpaint its original location, while ensuring image consistency by anchoring the edited image to be generated to the pixel-manipulated image as well as by introducing various consistency-preserving optimization techniques during inference. Experimental evaluations based on benchmark datasets as well as extensive visual comparisons show that in as few as 16 inference steps, PixelMan outperforms a range of state-of-the-art training-based and training-free methods (usually requiring 50 steps) on multiple consistent object editing tasks.

EiG-Search: Generating Edge-Induced Subgraphs for GNN Explanation in Linear Time

Understanding and explaining the predictions of Graph Neural Networks (GNNs), is crucial for enhancing their safety and trustworthiness. Subgraph-level explanations are gaining attention for their intuitive appeal. However, most existing subgraph-level explainers face efficiency challenges in explaining GNNs due to complex search processes. The key challenge is to find a balance between intuitiveness and efficiency while ensuring transparency. Additionally, these explainers usually induce subgraphs by nodes, which may introduce less-intuitive disconnected nodes in the subgraph-level explanations or omit many important subgraph structures. In this paper, we reveal that inducing subgraph explanations by edges is more comprehensive than other subgraph inducing techniques. We also emphasize the need of determining the subgraph explanation size for each data instance, as different data instances may involve different important substructures. Building upon these considerations, we introduce a training-free approach, named EiG-Search. We employ an efficient linear-time search algorithm over the edge-induced subgraphs, where the edges are ranked by an enhanced gradient-based importance. We conduct extensive experiments on a total of seven datasets, demonstrating its superior performance and efficiency both quantitatively and qualitatively over the leading baselines.

Building Optimal Neural Architectures using Interpretable Knowledge

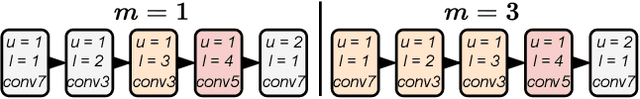
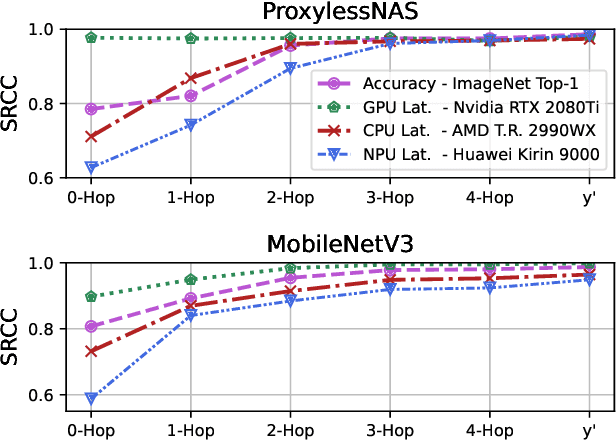
Neural Architecture Search is a costly practice. The fact that a search space can span a vast number of design choices with each architecture evaluation taking nontrivial overhead makes it hard for an algorithm to sufficiently explore candidate networks. In this paper, we propose AutoBuild, a scheme which learns to align the latent embeddings of operations and architecture modules with the ground-truth performance of the architectures they appear in. By doing so, AutoBuild is capable of assigning interpretable importance scores to architecture modules, such as individual operation features and larger macro operation sequences such that high-performance neural networks can be constructed without any need for search. Through experiments performed on state-of-the-art image classification, segmentation, and Stable Diffusion models, we show that by mining a relatively small set of evaluated architectures, AutoBuild can learn to build high-quality architectures directly or help to reduce search space to focus on relevant areas, finding better architectures that outperform both the original labeled ones and ones found by search baselines. Code available at https://github.com/Ascend-Research/AutoBuild

GOAt: Explaining Graph Neural Networks via Graph Output Attribution

Understanding the decision-making process of Graph Neural Networks (GNNs) is crucial to their interpretability. Most existing methods for explaining GNNs typically rely on training auxiliary models, resulting in the explanations remain black-boxed. This paper introduces Graph Output Attribution (GOAt), a novel method to attribute graph outputs to input graph features, creating GNN explanations that are faithful, discriminative, as well as stable across similar samples. By expanding the GNN as a sum of scalar products involving node features, edge features and activation patterns, we propose an efficient analytical method to compute contribution of each node or edge feature to each scalar product and aggregate the contributions from all scalar products in the expansion form to derive the importance of each node and edge. Through extensive experiments on synthetic and real-world data, we show that our method not only outperforms various state-ofthe-art GNN explainers in terms of the commonly used fidelity metric, but also exhibits stronger discriminability, and stability by a remarkable margin.

Ternary Singular Value Decomposition as a Better Parameterized Form in Linear Mapping

We present a simple yet novel parameterized form of linear mapping to achieves remarkable network compression performance: a pseudo SVD called Ternary SVD (TSVD). Unlike vanilla SVD, TSVD limits the $U$ and $V$ matrices in SVD to ternary matrices form in $\{\pm 1, 0\}$. This means that instead of using the expensive multiplication instructions, TSVD only requires addition instructions when computing $U(\cdot)$ and $V(\cdot)$. We provide direct and training transition algorithms for TSVD like Post Training Quantization and Quantization Aware Training respectively. Additionally, we analyze the convergence of the direct transition algorithms in theory. In experiments, we demonstrate that TSVD can achieve state-of-the-art network compression performance in various types of networks and tasks, including current baseline models such as ConvNext, Swim, BERT, and large language model like OPT.