An Efficient Data Analysis Method for Big Data using Multiple-Model Linear Regression

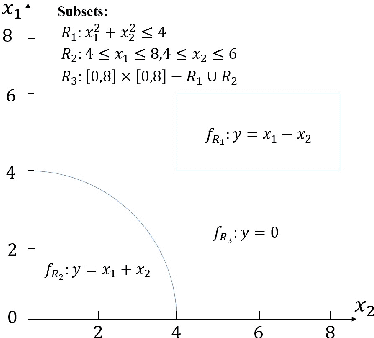
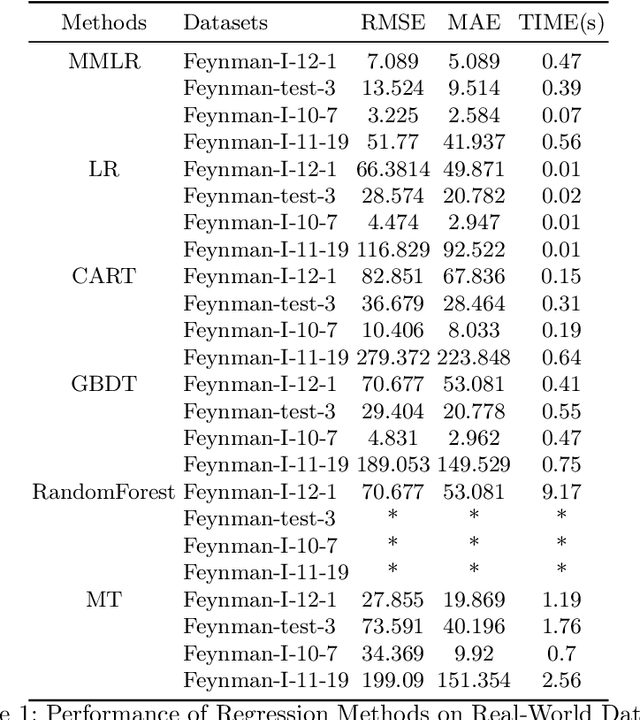
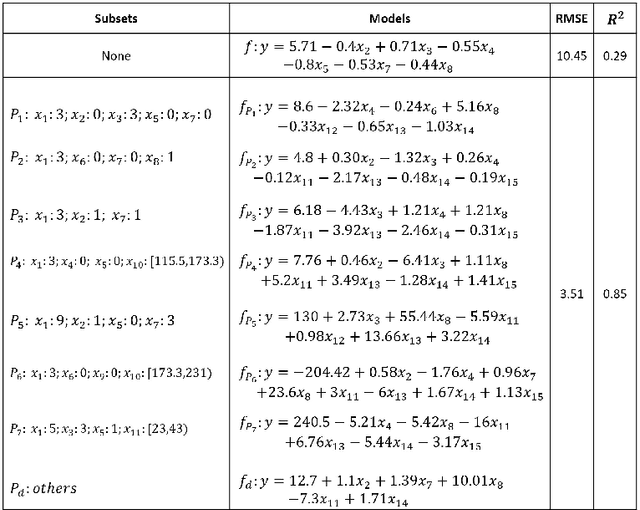
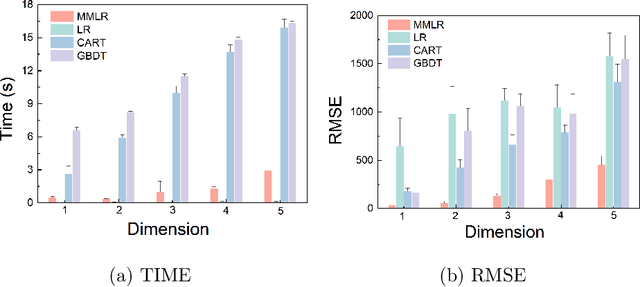
This paper introduces a new data analysis method for big data using a newly defined regression model named multiple model linear regression(MMLR), which separates input datasets into subsets and construct local linear regression models of them. The proposed data analysis method is shown to be more efficient and flexible than other regression based methods. This paper also proposes an approximate algorithm to construct MMLR models based on $(\epsilon,\delta)$-estimator, and gives mathematical proofs of the correctness and efficiency of MMLR algorithm, of which the time complexity is linear with respect to the size of input datasets. This paper also empirically implements the method on both synthetic and real-world datasets, the algorithm shows to have comparable performance to existing regression methods in many cases, while it takes almost the shortest time to provide a high prediction accuracy.

Rank-Regret Minimization

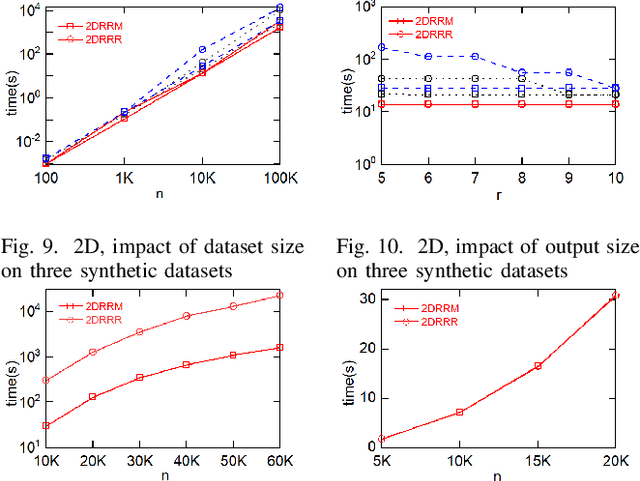
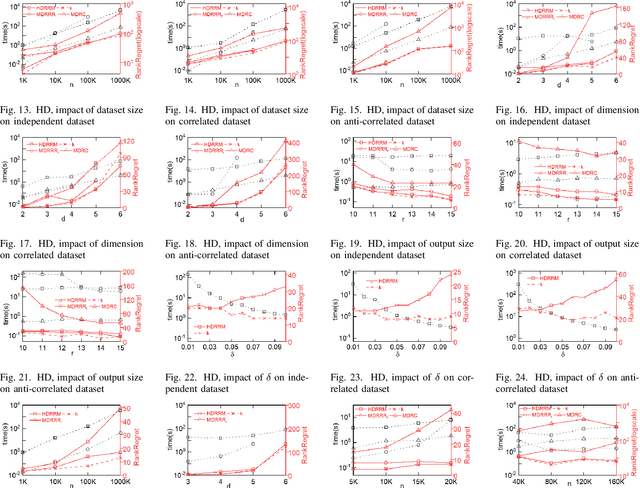
Multi-criteria decision-making often requires finding a small representative subset from the database. A recently proposed method is the regret minimization set (RMS) query. RMS returns a fixed size subset S of dataset D that minimizes the regret ratio of S (the difference between the score of top1 in S and the score of top-1 in D, for any possible utility function). Existing work showed that the regret-ratio is not able to accurately quantify the regret level of a user. Further, relative to the regret-ratio, users do understand the notion of rank. Consequently, it considered the problem of finding a minimal set S with at most k rank-regret (the minimal rank of tuples of S in the sorted list of D). Corresponding to RMS, we focus on the dual version of the above problem, defined as the rank-regret minimization (RRM) problem, which seeks to find a fixed size set S that minimizes the maximum rank-regret for all possible utility functions. Further, we generalize RRM and propose the restricted rank-regret minimization (RRRM) problem to minimize the rank-regret of S for functions in a restricted space. The solution for RRRM usually has a lower regret level and can better serve the specific preferences of some users. In 2D space, we design a dynamic programming algorithm 2DRRM to find the optimal solution for RRM. In HD space, we propose an algorithm HDRRM for RRM that bounds the output size and introduces a double approximation guarantee for rank-regret. Both 2DRRM and HDRRM can be generalized to the RRRM problem. Extensive experiments are performed on the synthetic and real datasets to verify the efficiency and effectiveness of our algorithms.

PCP Theorems, SETH and More: Towards Proving Sub-linear Time Inapproximability

In this paper we propose the PCP-like theorem for sub-linear time inapproximability. Abboud et al. have devised the distributed PCP framework for sub-quadratic time inapproximability. We show that the distributed PCP theorem can be generalized for proving arbitrary polynomial time inapproximability, but fails in the linear case. We prove the sub-linear PCP theorem by adapting from an MA-protocol for the Set Containment problem, and show how to use the theorem to prove both existing and new inapproximability results, exhibiting the power of the sub-linear PCP theorem. Considering the emerging research works on sub-linear time algorithms, the sub-linear PCP theorem is important in guiding the research in sub-linear time approximation algorithms.

ExperienceThinking: Hyperparameter Optimization with Budget Constraints

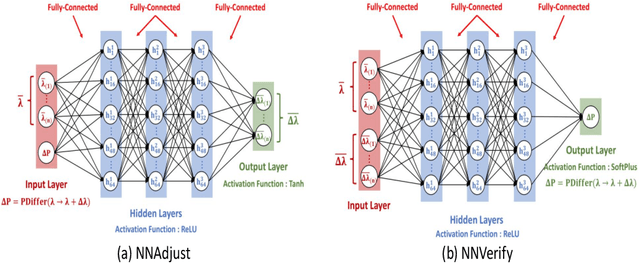
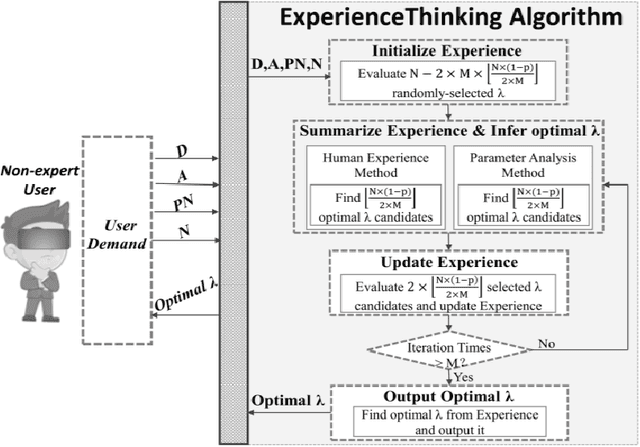
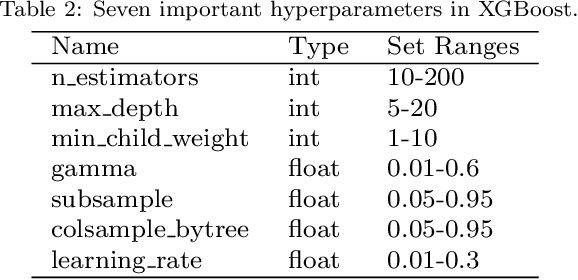
The problem of hyperparameter optimization exists widely in the real life and many common tasks can be transformed into it, such as neural architecture search and feature subset selection. Without considering various constraints, the existing hyperparameter tuning techniques can solve these problems effectively by traversing as many hyperparameter configurations as possible. However, because of the limited resources and budget, it is not feasible to evaluate so many kinds of configurations, which requires us to design effective algorithms to find a best possible hyperparameter configuration with a finite number of configuration evaluations. In this paper, we simulate human thinking processes and combine the merit of the existing techniques, and thus propose a new algorithm called ExperienceThinking, trying to solve this constrained hyperparameter optimization problem. In addition, we analyze the performances of 3 classical hyperparameter optimization algorithms with a finite number of configuration evaluations, and compare with that of ExperienceThinking. The experimental results show that our proposed algorithm provides superior results and has better performance.

Auto-Model: Utilizing Research Papers and HPO Techniques to Deal with the CASH problem

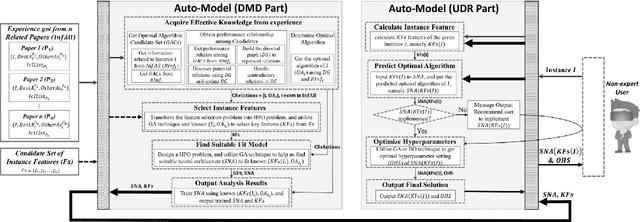
In many fields, a mass of algorithms with completely different hyperparameters have been developed to address the same type of problems. Choosing the algorithm and hyperparameter setting correctly can promote the overall performance greatly, but users often fail to do so due to the absence of knowledge. How to help users to effectively and quickly select the suitable algorithm and hyperparameter settings for the given task instance is an important research topic nowadays, which is known as the CASH problem. In this paper, we design the Auto-Model approach, which makes full use of known information in the related research paper and introduces hyperparameter optimization techniques, to solve the CASH problem effectively. Auto-Model tremendously reduces the cost of algorithm implementations and hyperparameter configuration space, and thus capable of dealing with the CASH problem efficiently and easily. To demonstrate the benefit of Auto-Model, we compare it with classical Auto-Weka approach. The experimental results show that our proposed approach can provide superior results and achieves better performance in a short time.

Autoregressive-Model-Based Methods for Online Time Series Prediction with Missing Values: an Experimental Evaluation

Time series prediction with missing values is an important problem of time series analysis since complete data is usually hard to obtain in many real-world applications. To model the generation of time series, autoregressive (AR) model is a basic and widely used one, which assumes that each observation in the time series is a noisy linear combination of some previous observations along with a constant shift. To tackle the problem of prediction with missing values, a number of methods were proposed based on various data models. For real application scenarios, how do these methods perform over different types of time series with different levels of data missing remains to be investigated. In this paper, we focus on online methods for AR-model-based time series prediction with missing values. We adapted five mainstream methods to fit in such a scenario. We make detailed discussion on each of them by introducing their core ideas about how to estimate the AR coefficients and their different strategies to deal with missing values. We also present algorithmic implementations for better understanding. In order to comprehensively evaluate these methods and do the comparison, we conduct experiments with various configurations of relative parameters over both synthetic and real data. From the experimental results, we derived several noteworthy conclusions and shows that imputation is a simple but reliable strategy to handle missing values in online prediction tasks.

Impacts of Dirty Data: and Experimental Evaluation

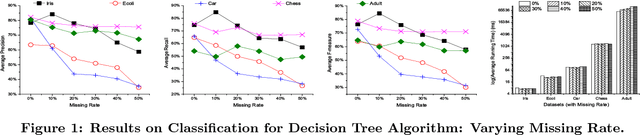
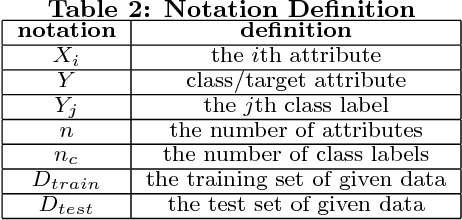
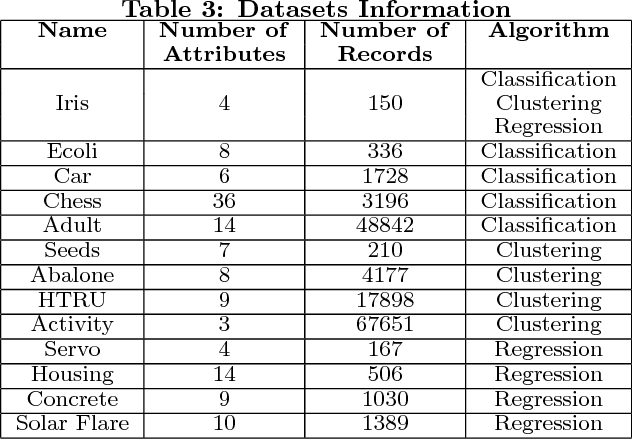
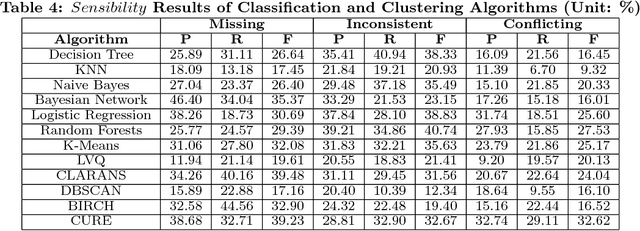
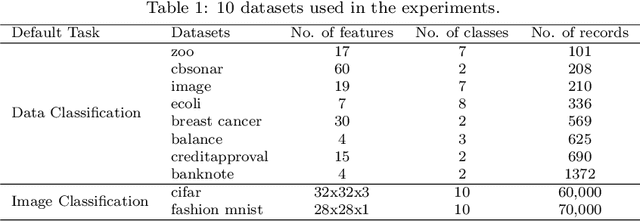
Data quality issues have attracted widespread attention due to the negative impacts of dirty data on data mining and machine learning results. The relationship between data quality and the accuracy of results could be applied on the selection of the appropriate algorithm with the consideration of data quality and the determination of the data share to clean. However, rare research has focused on exploring such relationship. Motivated by this, this paper conducts an experimental comparison for the effects of missing, inconsistent and conflicting data on classification, clustering, and regression algorithms. Based on the experimental findings, we provide guidelines for algorithm selection and data cleaning.