Xingxing Xiao
Rank-Regret Minimization
Nov 16, 2021
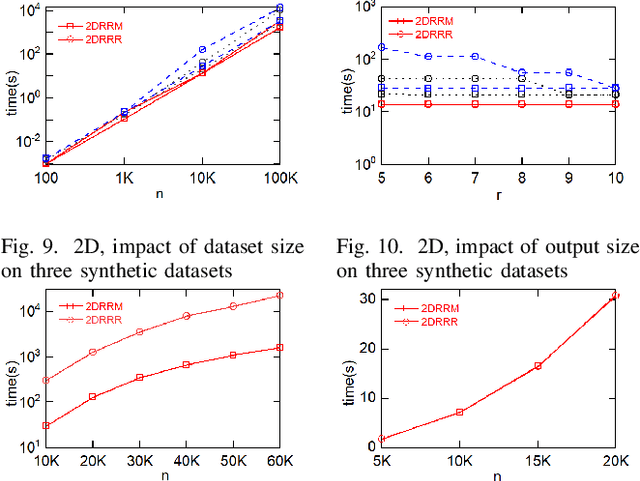
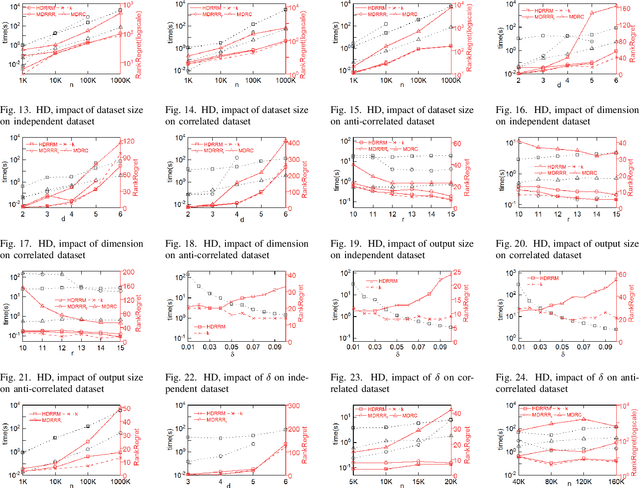

Abstract:Multi-criteria decision-making often requires finding a small representative subset from the database. A recently proposed method is the regret minimization set (RMS) query. RMS returns a fixed size subset S of dataset D that minimizes the regret ratio of S (the difference between the score of top1 in S and the score of top-1 in D, for any possible utility function). Existing work showed that the regret-ratio is not able to accurately quantify the regret level of a user. Further, relative to the regret-ratio, users do understand the notion of rank. Consequently, it considered the problem of finding a minimal set S with at most k rank-regret (the minimal rank of tuples of S in the sorted list of D). Corresponding to RMS, we focus on the dual version of the above problem, defined as the rank-regret minimization (RRM) problem, which seeks to find a fixed size set S that minimizes the maximum rank-regret for all possible utility functions. Further, we generalize RRM and propose the restricted rank-regret minimization (RRRM) problem to minimize the rank-regret of S for functions in a restricted space. The solution for RRRM usually has a lower regret level and can better serve the specific preferences of some users. In 2D space, we design a dynamic programming algorithm 2DRRM to find the optimal solution for RRM. In HD space, we propose an algorithm HDRRM for RRM that bounds the output size and introduces a double approximation guarantee for rank-regret. Both 2DRRM and HDRRM can be generalized to the RRRM problem. Extensive experiments are performed on the synthetic and real datasets to verify the efficiency and effectiveness of our algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge