VisCritic: Visual State Comparison as Process Reward for GUI Agents

GUI agents powered by vision-language models show strong potential for automating digital tasks, yet frequently fail in long-horizon scenarios due to the absence of step-level verification. Existing process reward models verify actions through textual reasoning alone, missing the visual nature of GUI state changes. We introduce VisCritic, a visual process reward framework that verifies agent actions by directly comparing pre-action and post-action screenshots in visual feature space. VisCritic employs a Siamese vision transformer to extract change-aware representations, coupled with an Action-Aware Critic Head that jointly evaluates action success, task progress, and error type. A critic-training data construction pipeline generates weakly supervised samples from existing trajectories without additional human labels for critic training. Experiments and offline analyses across five benchmarks demonstrate that VisCritic serves as a plug-and-play enhancement for diverse GUI agents, generally improving benchmark metrics while providing visual diagnostic cues.

SilentRetrieval: Hijacking Retrieval-Augmented Generation via Semantically-Preserving Adversarial Data Poisoning

Retrieval-Augmented Generation (RAG) mitigates LLM hallucinations but introduces a critical vulnerability: corpus integrity. We present SilentRetrieval, a two-stage data poisoning attack that hijacks RAG systems through adversarially crafted yet fluent documents. Stage 1 uses Coordinated Beam Search, a multi-token joint optimization method with a fluency-similarity objective, to keep a poisoned host document retrievable while constraining perplexity. Stage 2 uses Context-Adaptive Trigger Generation, a lightweight trigger-fusion step driven by a frozen LLM, to integrate manipulation triggers into document content. Under a one-poisoned-document-per-query evaluation with synthetic target answers, SilentRetrieval achieves 84.6%/81.3% HR@10 and 57.5%/54.8% ASR-LLM on Natural Questions and MS MARCO, while maintaining near-benign perplexity. Cross-model evaluation across four target LLMs shows nontrivial effectiveness under a fixed trigger generator, and transfer tests against unseen retrievers, including ColBERT and commercial embedding models, yield 64.7% average HR@10 under the same injected-corpus protocol. In a sampled Wikipedia-scale evaluation, SilentRetrieval retains 74.2% HR@10 at a 0.016% poisoning ratio. Combined retrieval-side and generation-side defenses reduce attack success substantially but incur a latency trade-off. Human evaluation shows substantially lower flag rates than disfluent baselines, while remaining numerically more suspicious than benign content at the current sample size.

JECA^2: Judgment-Explanation Consistent Adversarial Attack against Forensic Vision-Language Models

Forensic vision-language models (VLMs) have recently been developed to detect image tampering and provide natural-language explanations. However, their robustness against adversarial manipulation remains underexplored. Existing adversarial attacks typically aim to flip the model's binary judgment, while the accompanying explanation may still reveal forensic cues and contradict the attacked judgment. In this paper, we study judgment-explanation consistent adversarial attacks against forensic VLMs and propose JECA^2, a controlled white-box red-team diagnostic that jointly redirects visual attribution and aligns textual explanations with the target judgment. On the visual side, JECA^2 uses Grad-CAM-guided perturbations to divert attribution from tampered regions toward benign regions. On the textual side, it optimizes prompt embeddings toward authenticity-affirming semantics under a token-proximity constraint. Experiments on forensic VLM benchmarks show that JECA^2 achieves higher attack success and automated judgment-explanation consistency than implemented baselines under white-box threat settings, while transfer to closed-source VLMs remains measurable but limited. Our results highlight a consistency failure mode in explanation-based forensic VLMs and motivate future robustness evaluation beyond binary detection accuracy.

How Order-Sensitive Are LLMs? OrderProbe for Deterministic Structural Reconstruction

Large language models (LLMs) excel at semantic understanding, yet their ability to reconstruct internal structure from scrambled inputs remains underexplored. Sentence-level restoration is ill-posed for automated evaluation because multiple valid word orders often exist. We introduce OrderProbe, a deterministic benchmark for structural reconstruction using fixed four-character expressions in Chinese, Japanese, and Korean, which have a unique canonical order and thus support exact-match scoring. We further propose a diagnostic framework that evaluates models beyond recovery accuracy, including semantic fidelity, logical validity, consistency, robustness sensitivity, and information density. Experiments on twelve widely used LLMs show that structural reconstruction remains difficult even for frontier systems: zero-shot recovery frequently falls below 35%. We also observe a consistent dissociation between semantic recall and structural planning, suggesting that structural robustness is not an automatic byproduct of semantic competence.

Logarithmic Regret and Polynomial Scaling in Online Multi-step-ahead Prediction

This letter studies the problem of online multi-step-ahead prediction for unknown linear stochastic systems. Using conditional distribution theory, we derive an optimal parameterization of the prediction policy as a linear function of future inputs, past inputs, and past outputs. Based on this characterization, we propose an online least-squares algorithm to learn the policy and analyze its regret relative to the optimal model-based predictor. We show that the online algorithm achieves logarithmic regret with respect to the optimal Kalman filter in the multi-step setting. Furthermore, with new proof techniques, we establish an almost-sure regret bound that does not rely on fixed failure probabilities for sufficiently large horizons $N$. Finally, our analysis also reveals that, while the regret remains logarithmic in $N$, its constant factor grows polynomially with the prediction horizon $H$, with the polynomial order set by the largest Jordan block of eigenvalue 1 in the system matrix.

Direct3D-S2: Gigascale 3D Generation Made Easy with Spatial Sparse Attention

Generating high-resolution 3D shapes using volumetric representations such as Signed Distance Functions (SDFs) presents substantial computational and memory challenges. We introduce Direct3D-S2, a scalable 3D generation framework based on sparse volumes that achieves superior output quality with dramatically reduced training costs. Our key innovation is the Spatial Sparse Attention (SSA) mechanism, which greatly enhances the efficiency of Diffusion Transformer (DiT) computations on sparse volumetric data. SSA allows the model to effectively process large token sets within sparse volumes, substantially reducing computational overhead and achieving a 3.9x speedup in the forward pass and a 9.6x speedup in the backward pass. Our framework also includes a variational autoencoder (VAE) that maintains a consistent sparse volumetric format across input, latent, and output stages. Compared to previous methods with heterogeneous representations in 3D VAE, this unified design significantly improves training efficiency and stability. Our model is trained on public available datasets, and experiments demonstrate that Direct3D-S2 not only surpasses state-of-the-art methods in generation quality and efficiency, but also enables training at 1024 resolution using only 8 GPUs, a task typically requiring at least 32 GPUs for volumetric representations at 256 resolution, thus making gigascale 3D generation both practical and accessible. Project page: https://www.neural4d.com/research/direct3d-s2.

Model-free Online Learning for the Kalman Filter: Forgetting Factor and Logarithmic Regret

We consider the problem of online prediction for an unknown, non-explosive linear stochastic system. With a known system model, the optimal predictor is the celebrated Kalman filter. In the case of unknown systems, existing approaches based on recursive least squares and its variants may suffer from degraded performance due to the highly imbalanced nature of the regression model. This imbalance can easily lead to overfitting and thus degrade prediction accuracy. We tackle this problem by injecting an inductive bias into the regression model via {exponential forgetting}. While exponential forgetting is a common wisdom in online learning, it is typically used for re-weighting data. In contrast, our approach focuses on balancing the regression model. This achieves a better trade-off between {regression} and {regularization errors}, and simultaneously reduces the {accumulation error}. With new proof techniques, we also provide a sharper logarithmic regret bound of $O(\log^3 N)$, where $N$ is the number of observations.

Distributed Kalman Filter with Ultimately Accurate Fused Measurement Covariance

This paper investigates the distributed Kalman filter (DKF) for linear systems, with specific attention on measurement fusion, which is a typical way of information sharing and is vital for enhancing stability and improving estimation accuracy. We show that it is the mismatch between the fused measurement and the fused covariance that leads to performance degradation or inconsistency in previous consensus-based DKF algorithms. To address this issue, we introduce two fully distributed approaches for calculating the exact covariance of the fused measurements, building upon which the modified DKF algorithms are proposed. Moreover, the performance analysis of the modified algorithms is also provided under rather mild conditions, including the steady-state value of the estimation error covariance. We also show that due to the guaranteed consistency in the modified DKF algorithms, the steady-state estimation accuracy is significantly improved compared to classical DKF algorithms. Numerical experiments are carried out to validate the theoretical analysis and show the advantages of the proposed methods.

Observation of Periodic Systems: Bridge Centralized Kalman Filtering and Consensus-Based Distributed Filtering

Compared with linear time invariant systems, linear periodic system can describe the periodic processes arising from nature and engineering more precisely. However, the time-varying system parameters increase the difficulty of the research on periodic system, such as stabilization and observation. This paper aims to consider the observation problem of periodic systems by bridging two fundamental filtering algorithms for periodic systems with a sensor network: consensus-on-measurement-based distributed filtering (CMDF) and centralized Kalman filtering (CKF). Firstly, one mild convergence condition based on uniformly collective observability is established for CMDF, under which the filtering performance of CMDF can be formulated as a symmetric periodic positive semidefinite (SPPS) solution to a discrete-time periodic Lyapunov equation. Then, the closed form of the performance gap between CMDF and CKF is presented in terms of the information fusion steps and the consensus weights of the network. Moreover, it is pointed out that the estimation error covariance of CMDF exponentially converges to the centralized one with the fusion steps tending to infinity. Altogether, these new results establish a concise and specific relationship between distributed and centralized filterings, and formulate the trade-off between the communication cost and distributed filtering performance on periodic systems. Finally, the theoretical results are verified with numerical experiments.

Harmonic-Copuled Riccati Equations and its Applications in Distributed Filtering

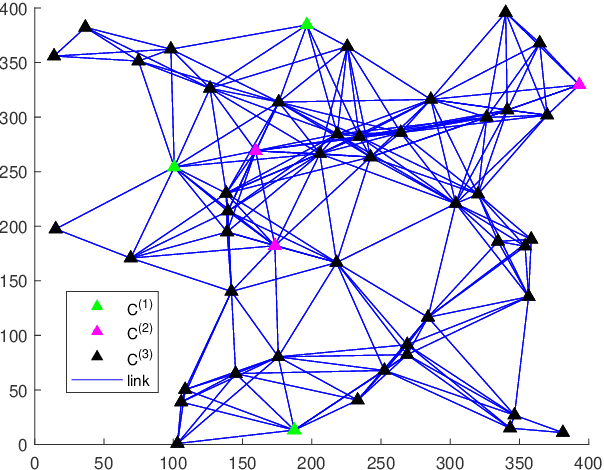
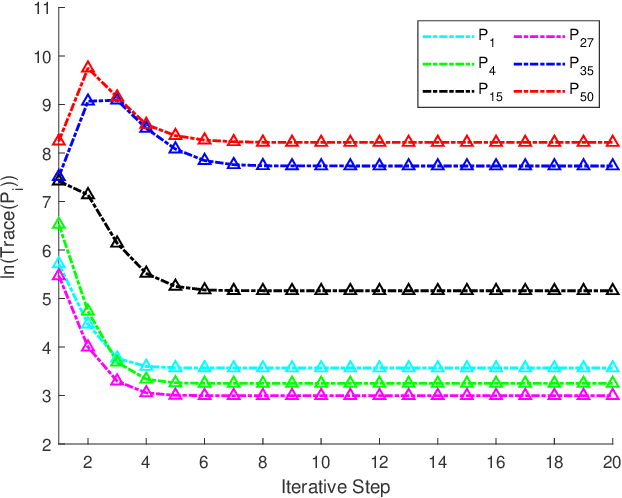
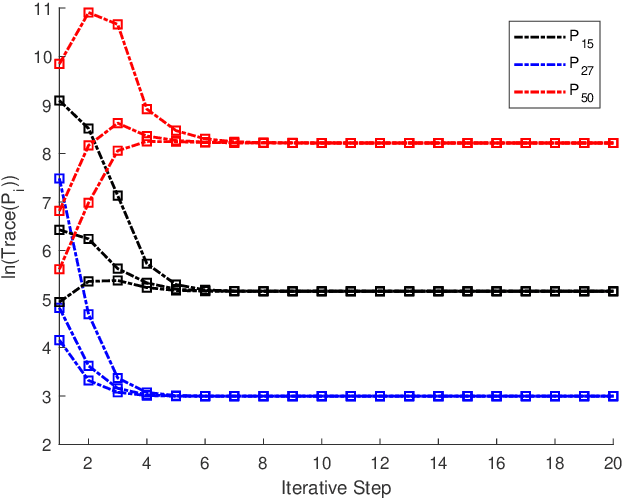
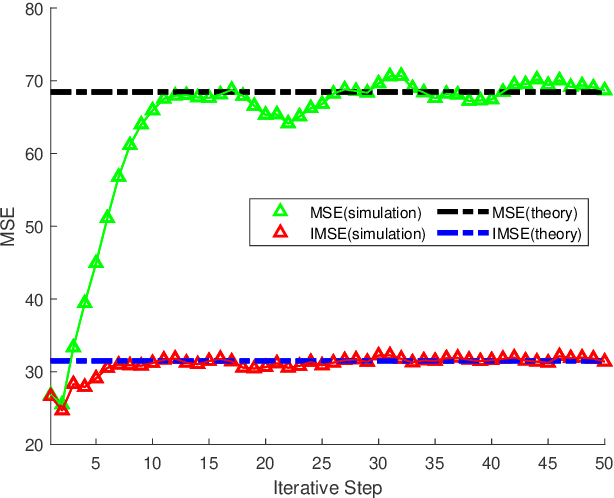
The coupled Riccati equations are cosisted of multiple Riccati-like equations with solutions coupled with each other, which can be applied to depict the properties of more complex systems such as markovian systems or multi-agent systems. This paper manages to formulate and investigate a new kind of coupled Riccati equations, called harmonic-coupled Riccati equations (HCRE), from the matrix iterative law of the consensus on information-based distributed filtering (CIDF) algortihm proposed in [1], where the solutions of the equations are coupled with harmonic means. Firstly, mild conditions of the existence and uniqueness of the solution to HCRE are induced with collective observability and primitiviness of weighting matrix. Then, it is proved that the matrix iterative law of CIDF will converge to the unique solution of the corresponding HCRE, hence can be used to obtain the solution to HCRE. Moreover, through applying the novel theory of HCRE, it is pointed out that the real estimation error covariance of CIDF will also become steady-state and the convergent value is simplified as the solution to a discrete time Lyapunov equation (DLE). Altogether, these new results develop the theory of the coupled Riccati equations, and provide a novel perspective on the performance analysis of CIDF algorithm, which sufficiently reduces the conservativeness of the evaluation techniques in the literature. Finally, the theoretical results are verified with numerical experiments.