Harmonic-Copuled Riccati Equations and its Applications in Distributed Filtering
Paper and Code
Nov 21, 2022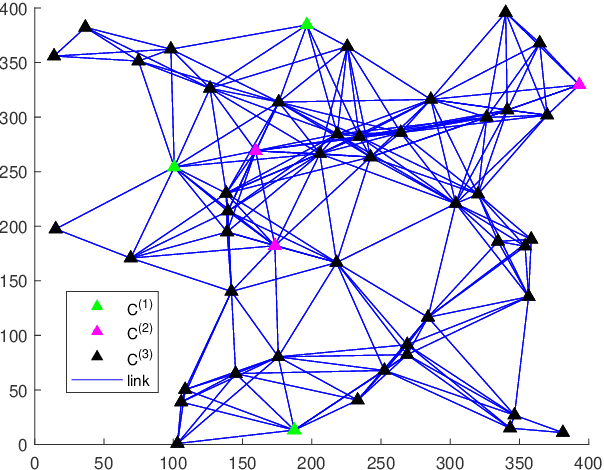
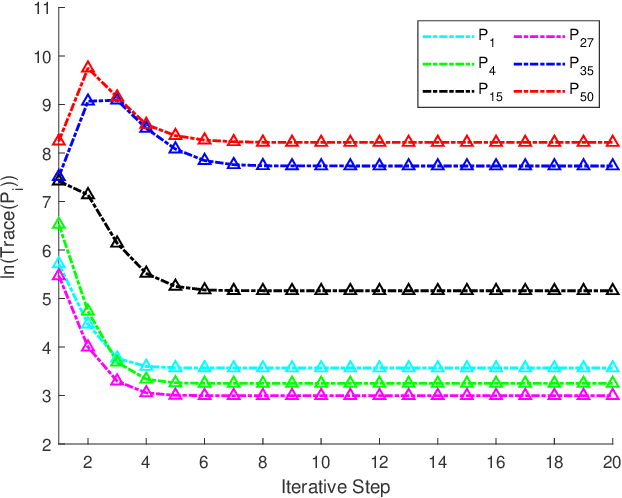
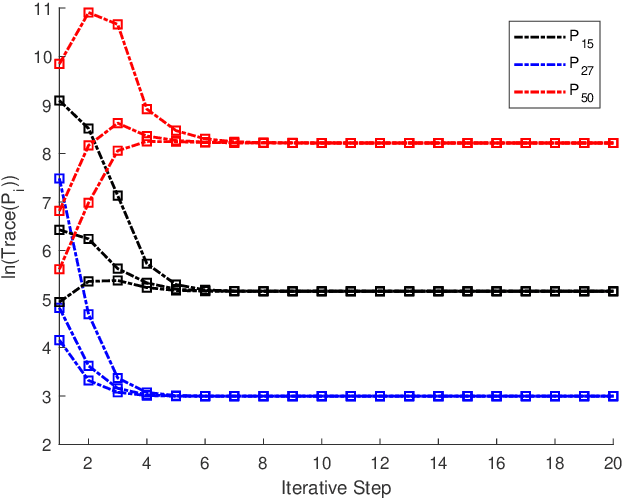
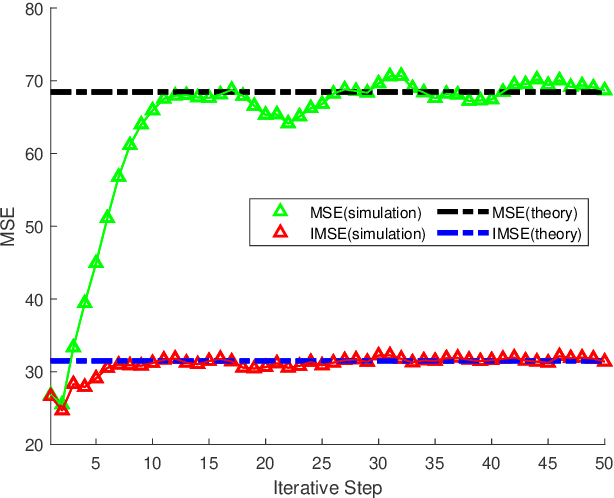
The coupled Riccati equations are cosisted of multiple Riccati-like equations with solutions coupled with each other, which can be applied to depict the properties of more complex systems such as markovian systems or multi-agent systems. This paper manages to formulate and investigate a new kind of coupled Riccati equations, called harmonic-coupled Riccati equations (HCRE), from the matrix iterative law of the consensus on information-based distributed filtering (CIDF) algortihm proposed in [1], where the solutions of the equations are coupled with harmonic means. Firstly, mild conditions of the existence and uniqueness of the solution to HCRE are induced with collective observability and primitiviness of weighting matrix. Then, it is proved that the matrix iterative law of CIDF will converge to the unique solution of the corresponding HCRE, hence can be used to obtain the solution to HCRE. Moreover, through applying the novel theory of HCRE, it is pointed out that the real estimation error covariance of CIDF will also become steady-state and the convergent value is simplified as the solution to a discrete time Lyapunov equation (DLE). Altogether, these new results develop the theory of the coupled Riccati equations, and provide a novel perspective on the performance analysis of CIDF algorithm, which sufficiently reduces the conservativeness of the evaluation techniques in the literature. Finally, the theoretical results are verified with numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge