Jhony K. Pontes
Deep Level Sets: Implicit Surface Representations for 3D Shape Inference
Jan 21, 2019
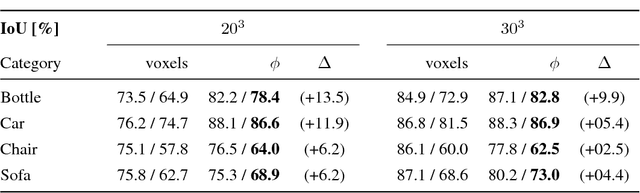


Abstract:Existing 3D surface representation approaches are unable to accurately classify pixels and their orientation lying on the boundary of an object. Thus resulting in coarse representations which usually require post-processing steps to extract 3D surface meshes. To overcome this limitation, we propose an end-to-end trainable model that directly predicts implicit surface representations of arbitrary topology by optimising a novel geometric loss function. Specifically, we propose to represent the output as an oriented level set of a continuous embedding function, and incorporate this in a deep end-to-end learning framework by introducing a variational shape inference formulation. We investigate the benefits of our approach on the task of 3D surface prediction and demonstrate its ability to produce a more accurate reconstruction compared to voxel-based representations. We further show that our model is flexible and can be applied to a variety of shape inference problems.
Learning Free-Form Deformations for 3D Object Reconstruction
Mar 29, 2018



Abstract:Representing 3D shape in deep learning frameworks in an accurate, efficient and compact manner still remains an open challenge. Most existing work addresses this issue by employing voxel-based representations. While these approaches benefit greatly from advances in computer vision by generalizing 2D convolutions to the 3D setting, they also have several considerable drawbacks. The computational complexity of voxel-encodings grows cubically with the resolution thus limiting such representations to low-resolution 3D reconstruction. In an attempt to solve this problem, point cloud representations have been proposed. Although point clouds are more efficient than voxel representations as they only cover surfaces rather than volumes, they do not encode detailed geometric information about relationships between points. In this paper we propose a method to learn free-form deformations (FFD) for the task of 3D reconstruction from a single image. By learning to deform points sampled from a high-quality mesh, our trained model can be used to produce arbitrarily dense point clouds or meshes with fine-grained geometry. We evaluate our proposed framework on both synthetic and real-world data and achieve state-of-the-art results on point-cloud and volumetric metrics. Additionally, we qualitatively demonstrate its applicability to label transferring for 3D semantic segmentation.
Image2Mesh: A Learning Framework for Single Image 3D Reconstruction
Nov 29, 2017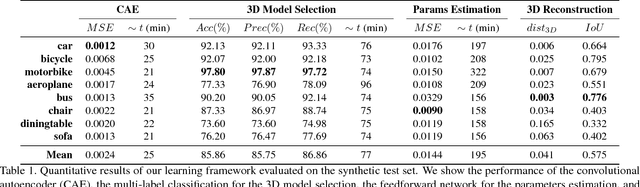

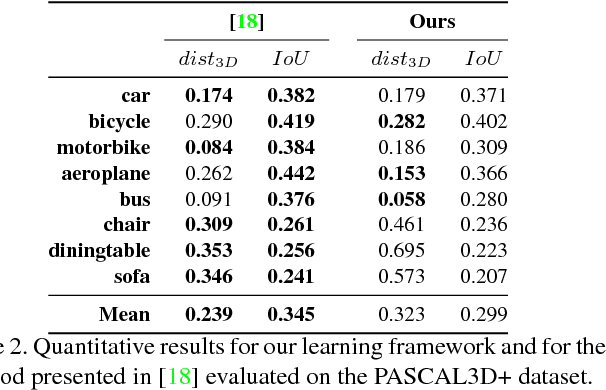

Abstract:One challenge that remains open in 3D deep learning is how to efficiently represent 3D data to feed deep networks. Recent works have relied on volumetric or point cloud representations, but such approaches suffer from a number of issues such as computational complexity, unordered data, and lack of finer geometry. This paper demonstrates that a mesh representation (i.e. vertices and faces to form polygonal surfaces) is able to capture fine-grained geometry for 3D reconstruction tasks. A mesh however is also unstructured data similar to point clouds. We address this problem by proposing a learning framework to infer the parameters of a compact mesh representation rather than learning from the mesh itself. This compact representation encodes a mesh using free-form deformation and a sparse linear combination of models allowing us to reconstruct 3D meshes from single images. In contrast to prior work, we do not rely on silhouettes and landmarks to perform 3D reconstruction. We evaluate our method on synthetic and real-world datasets with very promising results. Our framework efficiently reconstructs 3D objects in a low-dimensional way while preserving its important geometrical aspects.
Compact Model Representation for 3D Reconstruction
Jul 23, 2017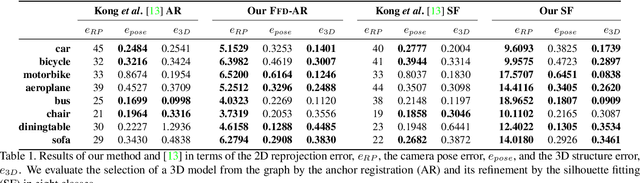
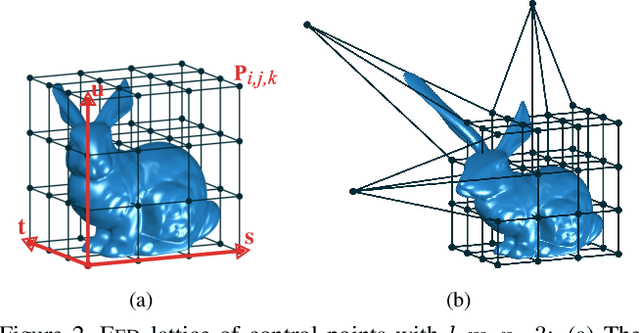
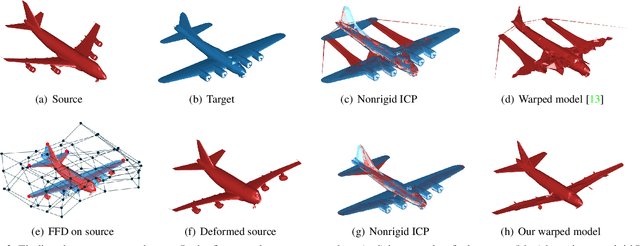

Abstract:3D reconstruction from 2D images is a central problem in computer vision. Recent works have been focusing on reconstruction directly from a single image. It is well known however that only one image cannot provide enough information for such a reconstruction. A prior knowledge that has been entertained are 3D CAD models due to its online ubiquity. A fundamental question is how to compactly represent millions of CAD models while allowing generalization to new unseen objects with fine-scaled geometry. We introduce an approach to compactly represent a 3D mesh. Our method first selects a 3D model from a graph structure by using a novel free-form deformation FFD 3D-2D registration, and then the selected 3D model is refined to best fit the image silhouette. We perform a comprehensive quantitative and qualitative analysis that demonstrates impressive dense and realistic 3D reconstruction from single images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge