Dominic Jack
Sparse Convolutions on Continuous Domains for Point Cloud and Event Stream Networks
Dec 02, 2020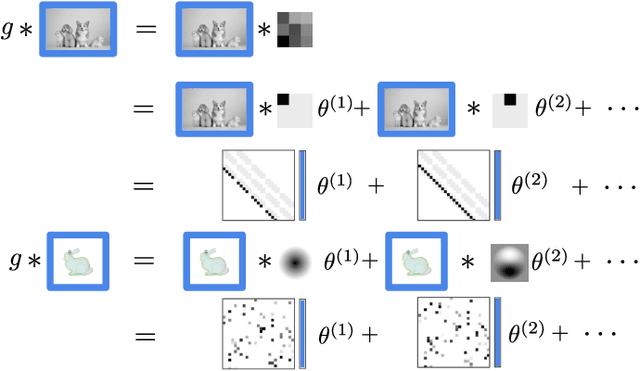

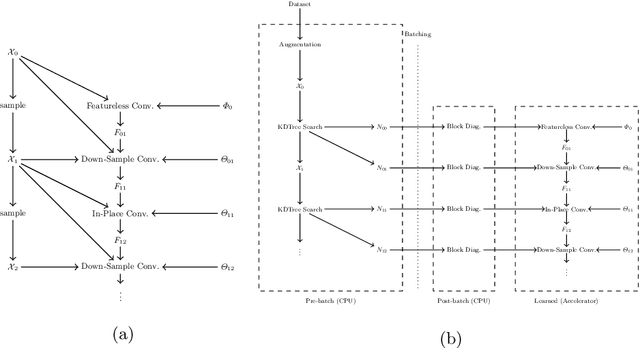

Abstract:Image convolutions have been a cornerstone of a great number of deep learning advances in computer vision. The research community is yet to settle on an equivalent operator for sparse, unstructured continuous data like point clouds and event streams however. We present an elegant sparse matrix-based interpretation of the convolution operator for these cases, which is consistent with the mathematical definition of convolution and efficient during training. On benchmark point cloud classification problems we demonstrate networks built with these operations can train an order of magnitude or more faster than top existing methods, whilst maintaining comparable accuracy and requiring a tiny fraction of the memory. We also apply our operator to event stream processing, achieving state-of-the-art results on multiple tasks with streams of hundreds of thousands of events.
Deep Level Sets: Implicit Surface Representations for 3D Shape Inference
Jan 21, 2019
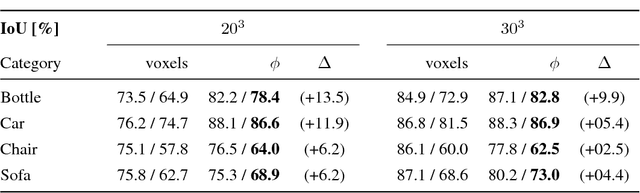


Abstract:Existing 3D surface representation approaches are unable to accurately classify pixels and their orientation lying on the boundary of an object. Thus resulting in coarse representations which usually require post-processing steps to extract 3D surface meshes. To overcome this limitation, we propose an end-to-end trainable model that directly predicts implicit surface representations of arbitrary topology by optimising a novel geometric loss function. Specifically, we propose to represent the output as an oriented level set of a continuous embedding function, and incorporate this in a deep end-to-end learning framework by introducing a variational shape inference formulation. We investigate the benefits of our approach on the task of 3D surface prediction and demonstrate its ability to produce a more accurate reconstruction compared to voxel-based representations. We further show that our model is flexible and can be applied to a variety of shape inference problems.
Learning Free-Form Deformations for 3D Object Reconstruction
Mar 29, 2018



Abstract:Representing 3D shape in deep learning frameworks in an accurate, efficient and compact manner still remains an open challenge. Most existing work addresses this issue by employing voxel-based representations. While these approaches benefit greatly from advances in computer vision by generalizing 2D convolutions to the 3D setting, they also have several considerable drawbacks. The computational complexity of voxel-encodings grows cubically with the resolution thus limiting such representations to low-resolution 3D reconstruction. In an attempt to solve this problem, point cloud representations have been proposed. Although point clouds are more efficient than voxel representations as they only cover surfaces rather than volumes, they do not encode detailed geometric information about relationships between points. In this paper we propose a method to learn free-form deformations (FFD) for the task of 3D reconstruction from a single image. By learning to deform points sampled from a high-quality mesh, our trained model can be used to produce arbitrarily dense point clouds or meshes with fine-grained geometry. We evaluate our proposed framework on both synthetic and real-world data and achieve state-of-the-art results on point-cloud and volumetric metrics. Additionally, we qualitatively demonstrate its applicability to label transferring for 3D semantic segmentation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge