The Future of Fundamental Science Led by Generative Closed-Loop Artificial Intelligence

Recent advances in machine learning and AI, including Generative AI and LLMs, are disrupting technological innovation, product development, and society as a whole. AI's contribution to technology can come from multiple approaches that require access to large training data sets and clear performance evaluation criteria, ranging from pattern recognition and classification to generative models. Yet, AI has contributed less to fundamental science in part because large data sets of high-quality data for scientific practice and model discovery are more difficult to access. Generative AI, in general, and Large Language Models in particular, may represent an opportunity to augment and accelerate the scientific discovery of fundamental deep science with quantitative models. Here we explore and investigate aspects of an AI-driven, automated, closed-loop approach to scientific discovery, including self-driven hypothesis generation and open-ended autonomous exploration of the hypothesis space. Integrating AI-driven automation into the practice of science would mitigate current problems, including the replication of findings, systematic production of data, and ultimately democratisation of the scientific process. Realising these possibilities requires a vision for augmented AI coupled with a diversity of AI approaches able to deal with fundamental aspects of causality analysis and model discovery while enabling unbiased search across the space of putative explanations. These advances hold the promise to unleash AI's potential for searching and discovering the fundamental structure of our world beyond what human scientists have been able to achieve. Such a vision would push the boundaries of new fundamental science rather than automatize current workflows and instead open doors for technological innovation to tackle some of the greatest challenges facing humanity today.

Algorithmic Probability-guided Supervised Machine Learning on Non-differentiable Spaces

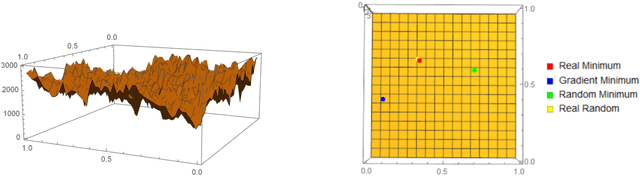
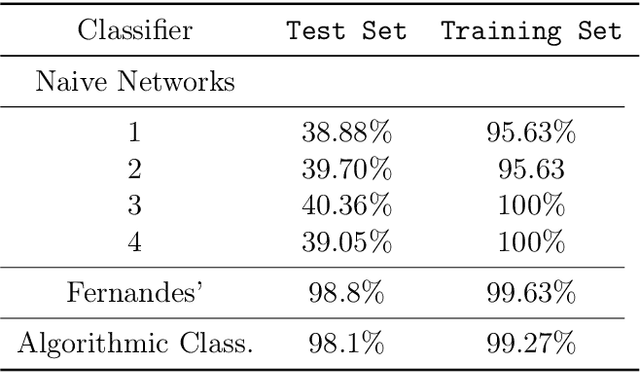
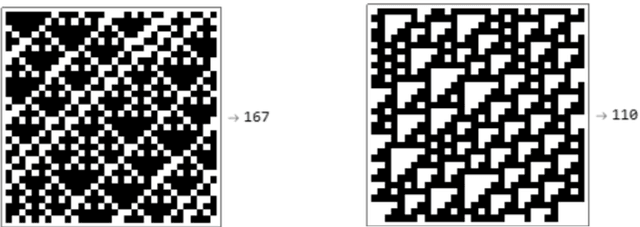
We show how complexity theory can be introduced in machine learning to help bring together apparently disparate areas of current research. We show that this new approach requires less training data and is more generalizable as it shows greater resilience to random attacks. We investigate the shape of the discrete algorithmic space when performing regression or classification using a loss function parametrized by algorithmic complexity, demonstrating that the property of differentiation is not necessary to achieve results similar to those obtained using differentiable programming approaches such as deep learning. In doing so we use examples which enable the two approaches to be compared (small, given the computational power required for estimations of algorithmic complexity). We find and report that (i) machine learning can successfully be performed on a non-smooth surface using algorithmic complexity; (ii) that parameter solutions can be found using an algorithmic-probability classifier, establishing a bridge between a fundamentally discrete theory of computability and a fundamentally continuous mathematical theory of optimization methods; (iii) a formulation of an algorithmically directed search technique in non-smooth manifolds can be defined and conducted; (iv) exploitation techniques and numerical methods for algorithmic search to navigate these discrete non-differentiable spaces can be performed; in application of the (a) identification of generative rules from data observations; (b) solutions to image classification problems more resilient against pixel attacks compared to neural networks; (c) identification of equation parameters from a small data-set in the presence of noise in continuous ODE system problem, (d) classification of Boolean NK networks by (1) network topology, (2) underlying Boolean function, and (3) number of incoming edges.

Algorithmic Causal Deconvolution of Intertwined Programs and Networks by Generative Mechanism

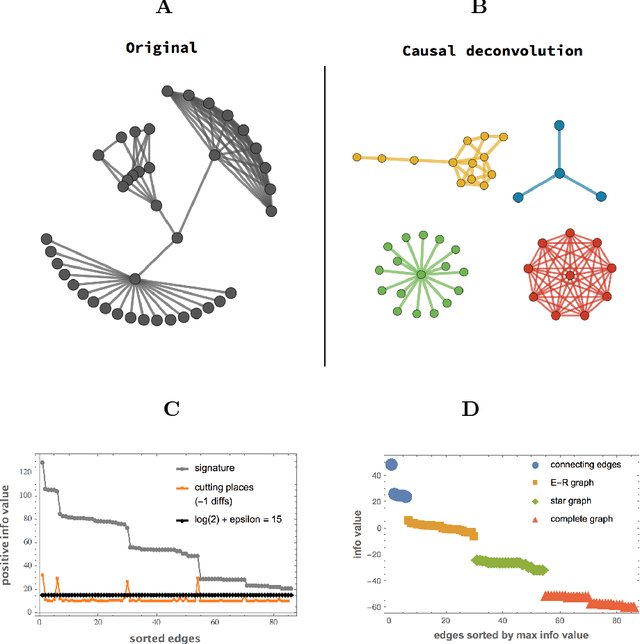
Complex data usually results from the interaction of objects produced by different generating mechanisms. Here we introduce a universal, unsupervised and parameter-free model-oriented approach, based upon the seminal concept of algorithmic probability, that decomposes an observation into its most likely algorithmic generative sources. Our approach uses a causal calculus to infer model representations. We demonstrate its ability to deconvolve interacting mechanisms regardless of whether the resultant objects are strings, space-time evolution diagrams, images or networks. While this is mostly a conceptual contribution and a novel framework, we provide numerical evidence evaluating the ability of our methods to separate data from observations produced by discrete dynamical systems such as cellular automata and complex networks. We think that these separating techniques can contribute to tackling the challenge of causation, thus complementing other statistically oriented approaches.

Learning Functions in Large Networks requires Modularity and produces Multi-Agent Dynamics

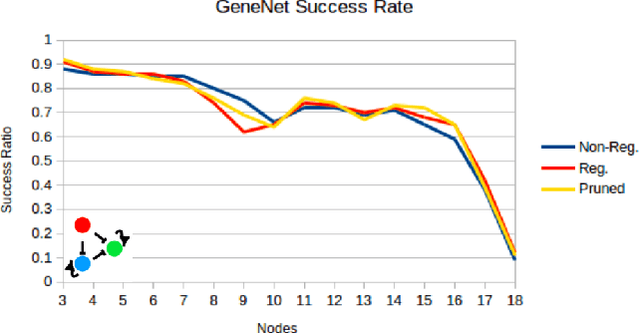
Networks are abundant in biological systems. Small sized over-represented network motifs have been discovered, and it has been suggested that these constitute functional building blocks. We ask whether larger dynamical network motifs exist in biological networks, thus contributing to the higher-order organization of a network. To end this, we introduce a gradient descent machine learning (ML) approach and genetic algorithms to learn larger functional motifs in contrast to an (unfeasible) exhaustive search. We use the French Flag (FF) and Switch functional motif as case studies motivated from biology. While our algorithm successfully learns large functional motifs, we identify a threshold size of approximately 20 nodes beyond which learning breaks down. Therefore we investigate the stability of the motifs. We find that the size of the real negative eigenvalues of the Jacobian decreases with increasing system size, thus conferring instability. Finally, without imposing learning an input-output for all the components of the network, we observe that unconstrained middle components of the network still learn the desired function, a form of homogeneous team learning. We conclude that the size limitation of learnability, most likely due to stability constraints, impose a definite requirement for modularity in networked systems while enabling team learning within unconstrained parts of the module. Thus, the observation that community structures and modularity are abundant in biological networks could be accounted for by a computational compositional network structure.

Causality, Information and Biological Computation: An algorithmic software approach to life, disease and the immune system

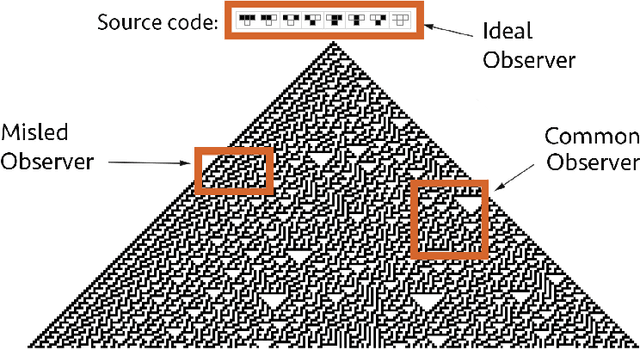
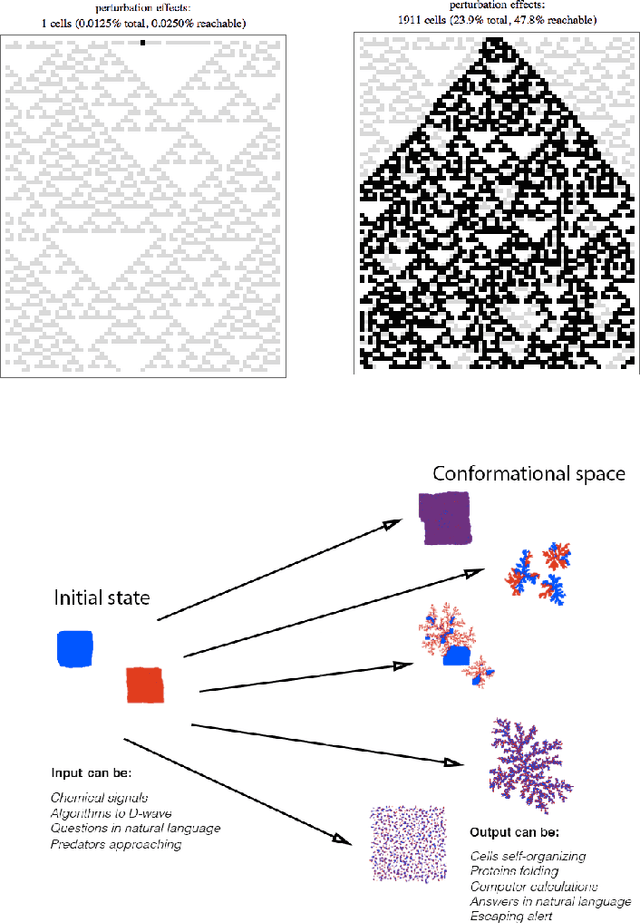
Biology has taken strong steps towards becoming a computer science aiming at reprogramming nature after the realisation that nature herself has reprogrammed organisms by harnessing the power of natural selection and the digital prescriptive nature of replicating DNA. Here we further unpack ideas related to computability, algorithmic information theory and software engineering, in the context of the extent to which biology can be (re)programmed, and with how we may go about doing so in a more systematic way with all the tools and concepts offered by theoretical computer science in a translation exercise from computing to molecular biology and back. These concepts provide a means to a hierarchical organization thereby blurring previously clear-cut lines between concepts like matter and life, or between tumour types that are otherwise taken as different and may not have however a different cause. This does not diminish the properties of life or make its components and functions less interesting. On the contrary, this approach makes for a more encompassing and integrated view of nature, one that subsumes observer and observed within the same system, and can generate new perspectives and tools with which to view complex diseases like cancer, approaching them afresh from a software-engineering viewpoint that casts evolution in the role of programmer, cells as computing machines, DNA and genes as instructions and computer programs, viruses as hacking devices, the immune system as a software debugging tool, and diseases as an information-theoretic battlefield where all these forces deploy. We show how information theory and algorithmic programming may explain fundamental mechanisms of life and death.

The Information-theoretic and Algorithmic Approach to Human, Animal and Artificial Cognition

We survey concepts at the frontier of research connecting artificial, animal and human cognition to computation and information processing---from the Turing test to Searle's Chinese Room argument, from Integrated Information Theory to computational and algorithmic complexity. We start by arguing that passing the Turing test is a trivial computational problem and that its pragmatic difficulty sheds light on the computational nature of the human mind more than it does on the challenge of artificial intelligence. We then review our proposed algorithmic information-theoretic measures for quantifying and characterizing cognition in various forms. These are capable of accounting for known biases in human behavior, thus vindicating a computational algorithmic view of cognition as first suggested by Turing, but this time rooted in the concept of algorithmic probability, which in turn is based on computational universality while being independent of computational model, and which has the virtue of being predictive and testable as a model theory of cognitive behavior.

Identifying the Relevant Nodes Without Learning the Model

We propose a method to identify all the nodes that are relevant to compute all the conditional probability distributions for a given set of nodes. Our method is simple, effcient, consistent, and does not require learning a Bayesian network first. Therefore, our method can be applied to high-dimensional databases, e.g. gene expression databases.