Adam Uccello
BEV-Patch-PF: Particle Filtering with BEV-Aerial Feature Matching for Off-Road Geo-Localization
Dec 17, 2025Abstract:We propose BEV-Patch-PF, a GPS-free sequential geo-localization system that integrates a particle filter with learned bird's-eye-view (BEV) and aerial feature maps. From onboard RGB and depth images, we construct a BEV feature map. For each 3-DoF particle pose hypothesis, we crop the corresponding patch from an aerial feature map computed from a local aerial image queried around the approximate location. BEV-Patch-PF computes a per-particle log-likelihood by matching the BEV feature to the aerial patch feature. On two real-world off-road datasets, our method achieves 7.5x lower absolute trajectory error (ATE) on seen routes and 7.0x lower ATE on unseen routes than a retrieval-based baseline, while maintaining accuracy under dense canopy and shadow. The system runs in real time at 10 Hz on an NVIDIA Tesla T4, enabling practical robot deployment.
Visual Representation Learning for Preference-Aware Path Planning
Sep 18, 2021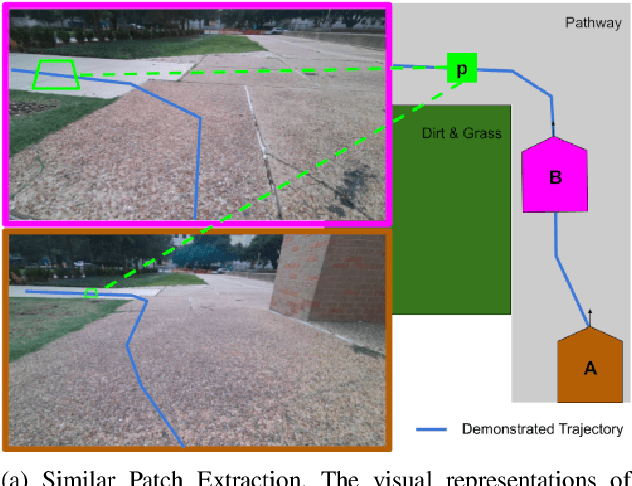

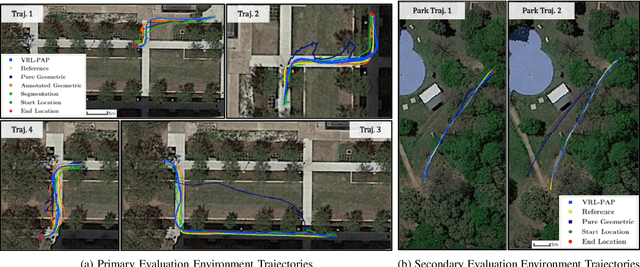
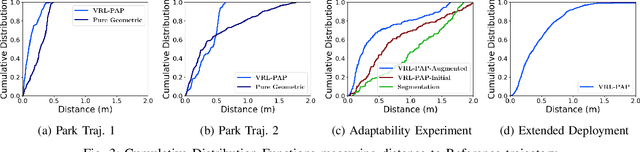
Abstract:Autonomous mobile robots deployed in outdoor environments must reason about different types of terrain for both safety (e.g., prefer dirt over mud) and deployer preferences (e.g., prefer dirt path over flower beds). Most existing solutions to this preference-aware path planning problem use semantic segmentation to classify terrain types from camera images, and then ascribe costs to each type. Unfortunately, there are three key limitations of such approaches -- they 1) require pre-enumeration of the discrete terrain types, 2) are unable to handle hybrid terrain types (e.g., grassy dirt), and 3) require expensive labelled data to train visual semantic segmentation. We introduce Visual Representation Learning for Preference-Aware Path Planning (VRL-PAP), an alternative approach that overcomes all three limitations: VRL-PAP leverages unlabeled human demonstrations of navigation to autonomously generate triplets for learning visual representations of terrain that are viewpoint invariant and encode terrain types in a continuous representation space. The learned representations are then used along with the same unlabeled human navigation demonstrations to learn a mapping from the representation space to terrain costs. At run time, VRL-PAP maps from images to representations and then representations to costs to perform preference-aware path planning. We present empirical results from challenging outdoor settings that demonstrate VRL-PAP 1) is successfully able to pick paths that reflect demonstrated preferences, 2) is comparable in execution to geometric navigation with a highly detailed manually annotated map (without requiring such annotations), 3) is able to generalize to novel terrain types with minimal additional unlabeled demonstrations.
Algorithmic Probability-guided Supervised Machine Learning on Non-differentiable Spaces
Oct 08, 2019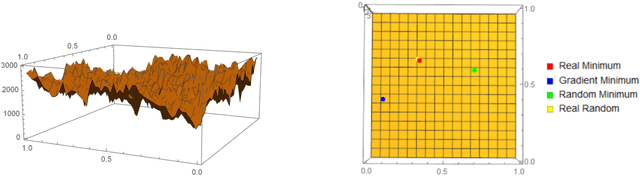
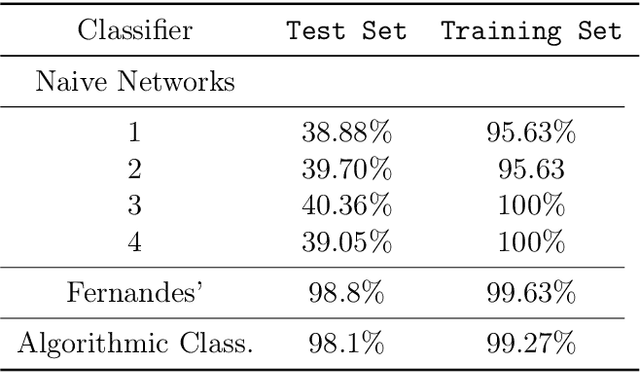
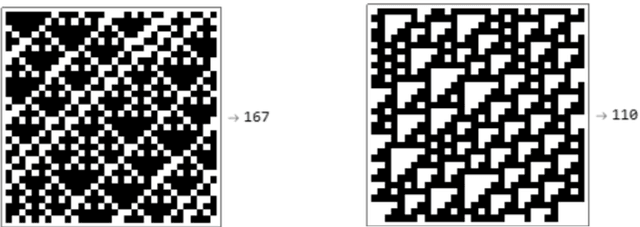

Abstract:We show how complexity theory can be introduced in machine learning to help bring together apparently disparate areas of current research. We show that this new approach requires less training data and is more generalizable as it shows greater resilience to random attacks. We investigate the shape of the discrete algorithmic space when performing regression or classification using a loss function parametrized by algorithmic complexity, demonstrating that the property of differentiation is not necessary to achieve results similar to those obtained using differentiable programming approaches such as deep learning. In doing so we use examples which enable the two approaches to be compared (small, given the computational power required for estimations of algorithmic complexity). We find and report that (i) machine learning can successfully be performed on a non-smooth surface using algorithmic complexity; (ii) that parameter solutions can be found using an algorithmic-probability classifier, establishing a bridge between a fundamentally discrete theory of computability and a fundamentally continuous mathematical theory of optimization methods; (iii) a formulation of an algorithmically directed search technique in non-smooth manifolds can be defined and conducted; (iv) exploitation techniques and numerical methods for algorithmic search to navigate these discrete non-differentiable spaces can be performed; in application of the (a) identification of generative rules from data observations; (b) solutions to image classification problems more resilient against pixel attacks compared to neural networks; (c) identification of equation parameters from a small data-set in the presence of noise in continuous ODE system problem, (d) classification of Boolean NK networks by (1) network topology, (2) underlying Boolean function, and (3) number of incoming edges.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge