Algorithmic Probability-guided Supervised Machine Learning on Non-differentiable Spaces

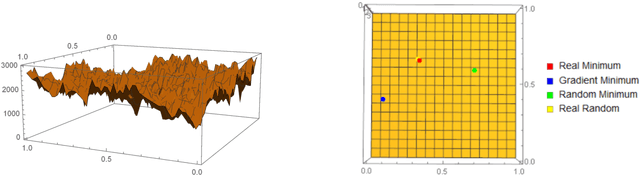
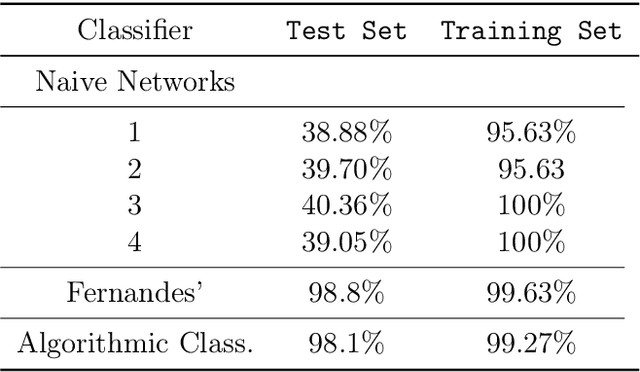
We show how complexity theory can be introduced in machine learning to help bring together apparently disparate areas of current research. We show that this new approach requires less training data and is more generalizable as it shows greater resilience to random attacks. We investigate the shape of the discrete algorithmic space when performing regression or classification using a loss function parametrized by algorithmic complexity, demonstrating that the property of differentiation is not necessary to achieve results similar to those obtained using differentiable programming approaches such as deep learning. In doing so we use examples which enable the two approaches to be compared (small, given the computational power required for estimations of algorithmic complexity). We find and report that (i) machine learning can successfully be performed on a non-smooth surface using algorithmic complexity; (ii) that parameter solutions can be found using an algorithmic-probability classifier, establishing a bridge between a fundamentally discrete theory of computability and a fundamentally continuous mathematical theory of optimization methods; (iii) a formulation of an algorithmically directed search technique in non-smooth manifolds can be defined and conducted; (iv) exploitation techniques and numerical methods for algorithmic search to navigate these discrete non-differentiable spaces can be performed; in application of the (a) identification of generative rules from data observations; (b) solutions to image classification problems more resilient against pixel attacks compared to neural networks; (c) identification of equation parameters from a small data-set in the presence of noise in continuous ODE system problem, (d) classification of Boolean NK networks by (1) network topology, (2) underlying Boolean function, and (3) number of incoming edges.

Coding-theorem Like Behaviour and Emergence of the Universal Distribution from Resource-bounded Algorithmic Probability

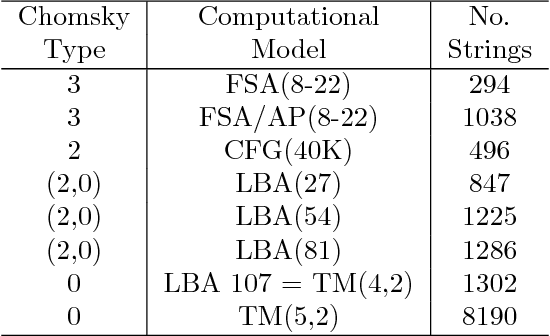
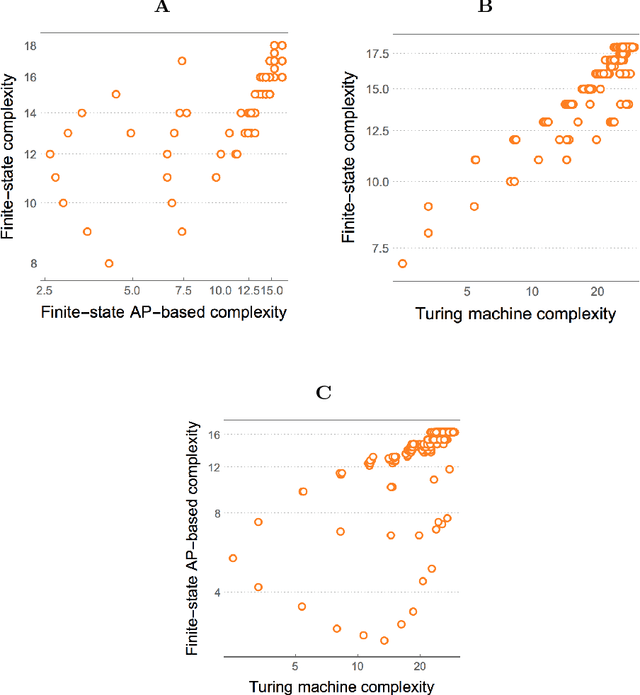
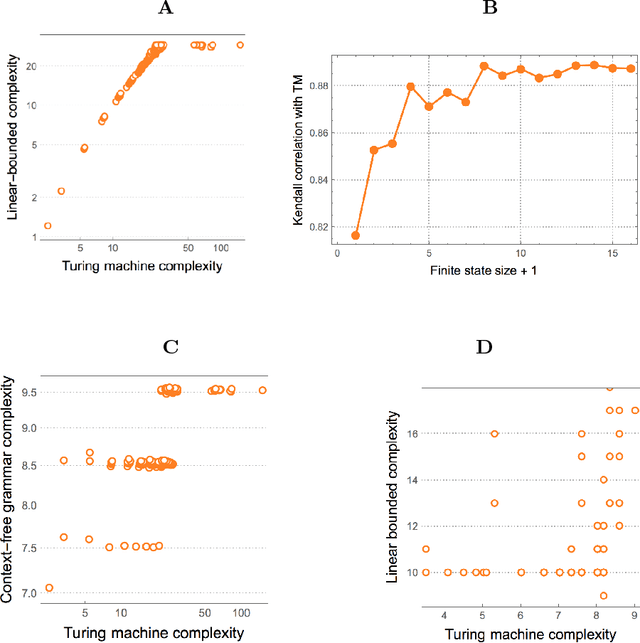
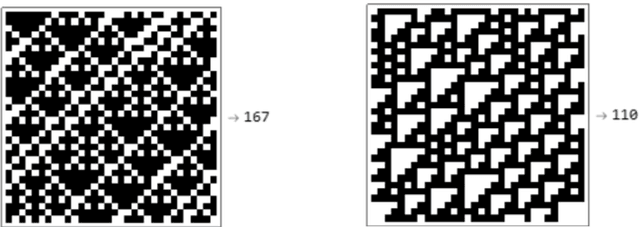
Previously referred to as `miraculous' in the scientific literature because of its powerful properties and its wide application as optimal solution to the problem of induction/inference, (approximations to) Algorithmic Probability (AP) and the associated Universal Distribution are (or should be) of the greatest importance in science. Here we investigate the emergence, the rates of emergence and convergence, and the Coding-theorem like behaviour of AP in Turing-subuniversal models of computation. We investigate empirical distributions of computing models in the Chomsky hierarchy. We introduce measures of algorithmic probability and algorithmic complexity based upon resource-bounded computation, in contrast to previously thoroughly investigated distributions produced from the output distribution of Turing machines. This approach allows for numerical approximations to algorithmic (Kolmogorov-Chaitin) complexity-based estimations at each of the levels of a computational hierarchy. We demonstrate that all these estimations are correlated in rank and that they converge both in rank and values as a function of computational power, despite fundamental differences between computational models. In the context of natural processes that operate below the Turing universal level because of finite resources and physical degradation, the investigation of natural biases stemming from algorithmic rules may shed light on the distribution of outcomes. We show that up to 60\% of the simplicity/complexity bias in distributions produced even by the weakest of the computational models can be accounted for by Algorithmic Probability in its approximation to the Universal Distribution.

Rare Speed-up in Automatic Theorem Proving Reveals Tradeoff Between Computational Time and Information Value

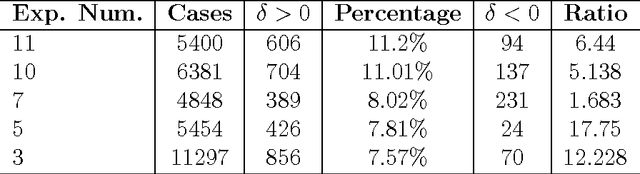
We show that strategies implemented in automatic theorem proving involve an interesting tradeoff between execution speed, proving speedup/computational time and usefulness of information. We advance formal definitions for these concepts by way of a notion of normality related to an expected (optimal) theoretical speedup when adding useful information (other theorems as axioms), as compared with actual strategies that can be effectively and efficiently implemented. We propose the existence of an ineluctable tradeoff between this normality and computational time complexity. The argument quantifies the usefulness of information in terms of (positive) speed-up. The results disclose a kind of no-free-lunch scenario and a tradeoff of a fundamental nature. The main theorem in this paper together with the numerical experiment---undertaken using two different automatic theorem provers AProS and Prover9 on random theorems of propositional logic---provide strong theoretical and empirical arguments for the fact that finding new useful information for solving a specific problem (theorem) is, in general, as hard as the problem (theorem) itself.