Rare Speed-up in Automatic Theorem Proving Reveals Tradeoff Between Computational Time and Information Value
Paper and Code
Jun 14, 2015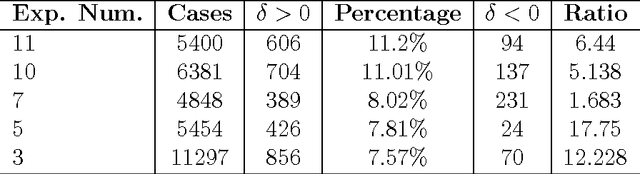



We show that strategies implemented in automatic theorem proving involve an interesting tradeoff between execution speed, proving speedup/computational time and usefulness of information. We advance formal definitions for these concepts by way of a notion of normality related to an expected (optimal) theoretical speedup when adding useful information (other theorems as axioms), as compared with actual strategies that can be effectively and efficiently implemented. We propose the existence of an ineluctable tradeoff between this normality and computational time complexity. The argument quantifies the usefulness of information in terms of (positive) speed-up. The results disclose a kind of no-free-lunch scenario and a tradeoff of a fundamental nature. The main theorem in this paper together with the numerical experiment---undertaken using two different automatic theorem provers AProS and Prover9 on random theorems of propositional logic---provide strong theoretical and empirical arguments for the fact that finding new useful information for solving a specific problem (theorem) is, in general, as hard as the problem (theorem) itself.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge