Coding-theorem Like Behaviour and Emergence of the Universal Distribution from Resource-bounded Algorithmic Probability
Paper and Code
Apr 13, 2018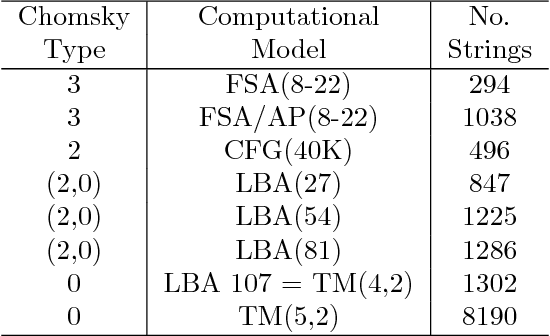
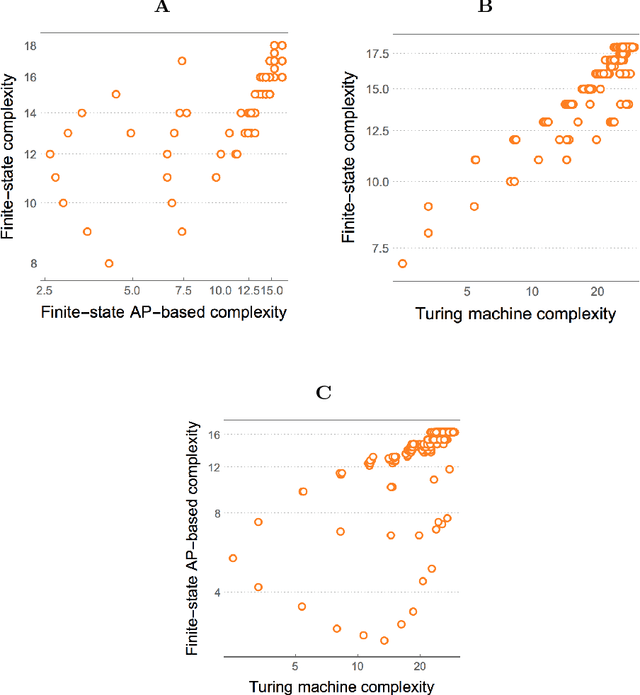
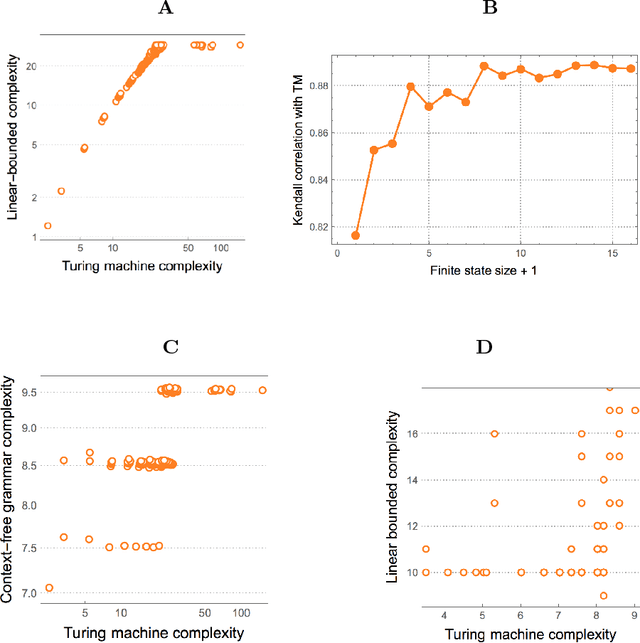

Previously referred to as `miraculous' in the scientific literature because of its powerful properties and its wide application as optimal solution to the problem of induction/inference, (approximations to) Algorithmic Probability (AP) and the associated Universal Distribution are (or should be) of the greatest importance in science. Here we investigate the emergence, the rates of emergence and convergence, and the Coding-theorem like behaviour of AP in Turing-subuniversal models of computation. We investigate empirical distributions of computing models in the Chomsky hierarchy. We introduce measures of algorithmic probability and algorithmic complexity based upon resource-bounded computation, in contrast to previously thoroughly investigated distributions produced from the output distribution of Turing machines. This approach allows for numerical approximations to algorithmic (Kolmogorov-Chaitin) complexity-based estimations at each of the levels of a computational hierarchy. We demonstrate that all these estimations are correlated in rank and that they converge both in rank and values as a function of computational power, despite fundamental differences between computational models. In the context of natural processes that operate below the Turing universal level because of finite resources and physical degradation, the investigation of natural biases stemming from algorithmic rules may shed light on the distribution of outcomes. We show that up to 60\% of the simplicity/complexity bias in distributions produced even by the weakest of the computational models can be accounted for by Algorithmic Probability in its approximation to the Universal Distribution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge