Personalized Public Policy Analysis in Social Sciences using Causal-Graphical Normalizing Flows

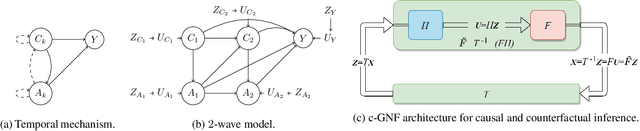
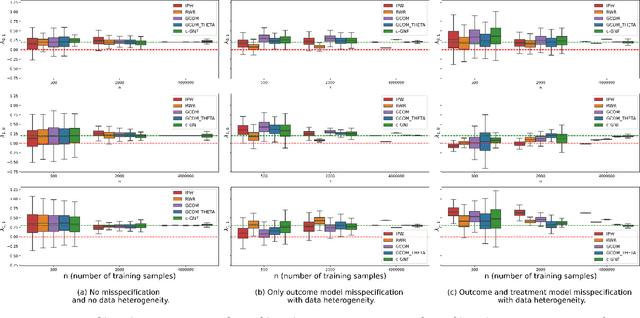
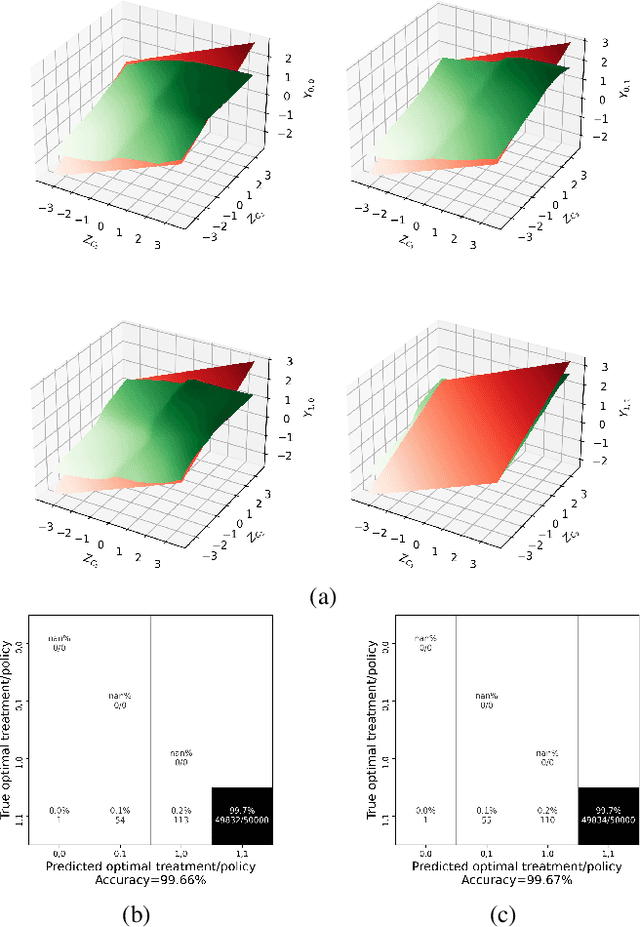
Structural Equation/Causal Models (SEMs/SCMs) are widely used in epidemiology and social sciences to identify and analyze the average treatment effect (ATE) and conditional ATE (CATE). Traditional causal effect estimation methods such as Inverse Probability Weighting (IPW) and more recently Regression-With-Residuals (RWR) are widely used - as they avoid the challenging task of identifying the SCM parameters - to estimate ATE and CATE. However, much work remains before traditional estimation methods can be used for counterfactual inference, and for the benefit of Personalized Public Policy Analysis (P$^3$A) in the social sciences. While doctors rely on personalized medicine to tailor treatments to patients in laboratory settings (relatively closed systems), P$^3$A draws inspiration from such tailoring but adapts it for open social systems. In this article, we develop a method for counterfactual inference that we name causal-Graphical Normalizing Flow (c-GNF), facilitating P$^3$A. First, we show how c-GNF captures the underlying SCM without making any assumption about functional forms. Second, we propose a novel dequantization trick to deal with discrete variables, which is a limitation of normalizing flows in general. Third, we demonstrate in experiments that c-GNF performs on-par with IPW and RWR in terms of bias and variance for estimating the ATE, when the true functional forms are known, and better when they are unknown. Fourth and most importantly, we conduct counterfactual inference with c-GNFs, demonstrating promising empirical performance. Because IPW and RWR, like other traditional methods, lack the capability of counterfactual inference, c-GNFs will likely play a major role in tailoring personalized treatment, facilitating P$^3$A, optimizing social interventions - in contrast to the current `one-size-fits-all' approach of existing methods.

Combinatorial Optimization by Learning and Simulation of Bayesian Networks

This paper shows how the Bayesian network paradigm can be used in order to solve combinatorial optimization problems. To do it some methods of structure learning from data and simulation of Bayesian networks are inserted inside Estimation of Distribution Algorithms (EDA). EDA are a new tool for evolutionary computation in which populations of individuals are created by estimation and simulation of the joint probability distribution of the selected individuals. We propose new approaches to EDA for combinatorial optimization based on the theory of probabilistic graphical models. Experimental results are also presented.

On Local Optima in Learning Bayesian Networks

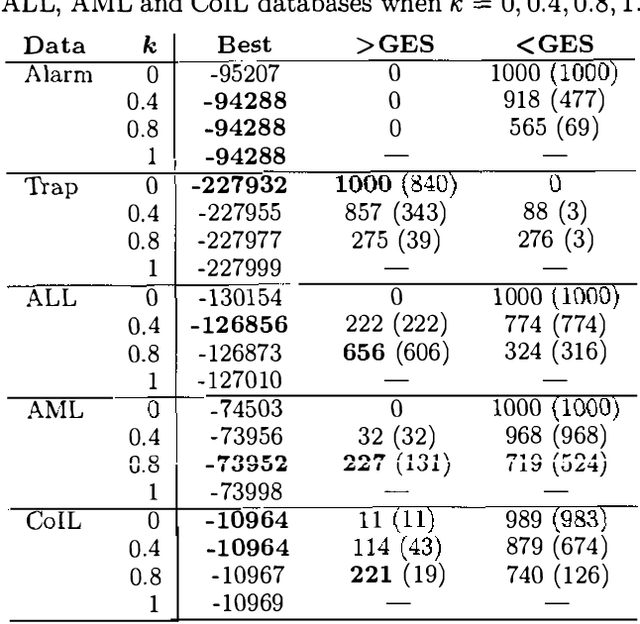
This paper proposes and evaluates the k-greedy equivalence search algorithm (KES) for learning Bayesian networks (BNs) from complete data. The main characteristic of KES is that it allows a trade-off between greediness and randomness, thus exploring different good local optima. When greediness is set at maximum, KES corresponds to the greedy equivalence search algorithm (GES). When greediness is kept at minimum, we prove that under mild assumptions KES asymptotically returns any inclusion optimal BN with nonzero probability. Experimental results for both synthetic and real data are reported showing that KES often finds a better local optima than GES. Moreover, we use KES to experimentally confirm that the number of different local optima is often huge.

Identifying the Relevant Nodes Without Learning the Model

We propose a method to identify all the nodes that are relevant to compute all the conditional probability distributions for a given set of nodes. Our method is simple, effcient, consistent, and does not require learning a Bayesian network first. Therefore, our method can be applied to high-dimensional databases, e.g. gene expression databases.

Reading Dependencies from Polytree-Like Bayesian Networks

We present a graphical criterion for reading dependencies from the minimal directed independence map G of a graphoid p when G is a polytree and p satisfies composition and weak transitivity. We prove that the criterion is sound and complete. We argue that assuming composition and weak transitivity is not too restrictive.