Personalized Public Policy Analysis in Social Sciences using Causal-Graphical Normalizing Flows

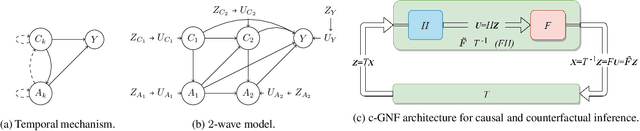
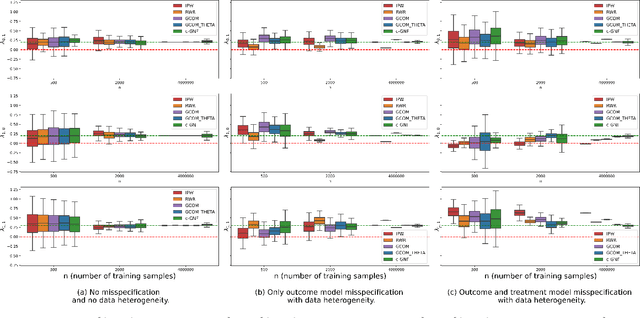
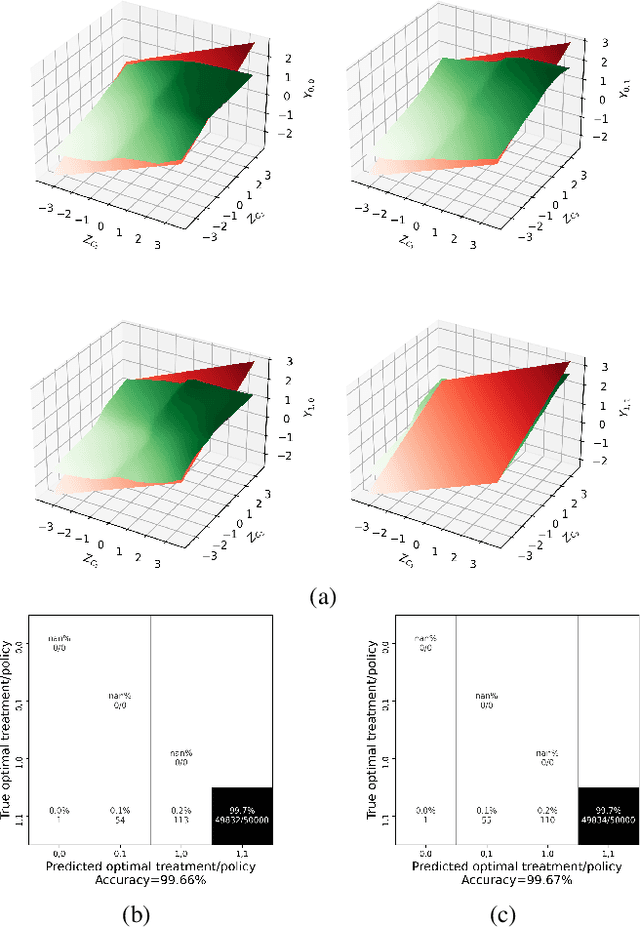
Structural Equation/Causal Models (SEMs/SCMs) are widely used in epidemiology and social sciences to identify and analyze the average treatment effect (ATE) and conditional ATE (CATE). Traditional causal effect estimation methods such as Inverse Probability Weighting (IPW) and more recently Regression-With-Residuals (RWR) are widely used - as they avoid the challenging task of identifying the SCM parameters - to estimate ATE and CATE. However, much work remains before traditional estimation methods can be used for counterfactual inference, and for the benefit of Personalized Public Policy Analysis (P$^3$A) in the social sciences. While doctors rely on personalized medicine to tailor treatments to patients in laboratory settings (relatively closed systems), P$^3$A draws inspiration from such tailoring but adapts it for open social systems. In this article, we develop a method for counterfactual inference that we name causal-Graphical Normalizing Flow (c-GNF), facilitating P$^3$A. First, we show how c-GNF captures the underlying SCM without making any assumption about functional forms. Second, we propose a novel dequantization trick to deal with discrete variables, which is a limitation of normalizing flows in general. Third, we demonstrate in experiments that c-GNF performs on-par with IPW and RWR in terms of bias and variance for estimating the ATE, when the true functional forms are known, and better when they are unknown. Fourth and most importantly, we conduct counterfactual inference with c-GNFs, demonstrating promising empirical performance. Because IPW and RWR, like other traditional methods, lack the capability of counterfactual inference, c-GNFs will likely play a major role in tailoring personalized treatment, facilitating P$^3$A, optimizing social interventions - in contrast to the current `one-size-fits-all' approach of existing methods.