Improved learning of Bayesian networks

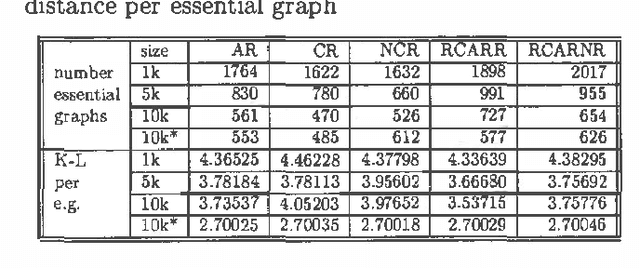
The search space of Bayesian Network structures is usually defined as Acyclic Directed Graphs (DAGs) and the search is done by local transformations of DAGs. But the space of Bayesian Networks is ordered by DAG Markov model inclusion and it is natural to consider that a good search policy should take this into account. First attempt to do this (Chickering 1996) was using equivalence classes of DAGs instead of DAGs itself. This approach produces better results but it is significantly slower. We present a compromise between these two approaches. It uses DAGs to search the space in such a way that the ordering by inclusion is taken into account. This is achieved by repetitive usage of local moves within the equivalence class of DAGs. We show that this new approach produces better results than the original DAGs approach without substantial change in time complexity. We present empirical results, within the framework of heuristic search and Markov Chain Monte Carlo, provided through the Alarm dataset.

On characterizing Inclusion of Bayesian Networks

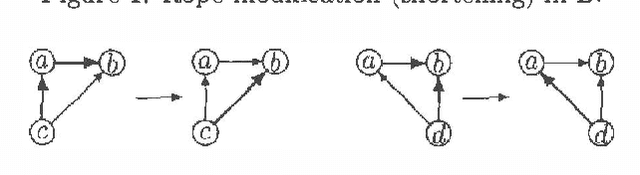
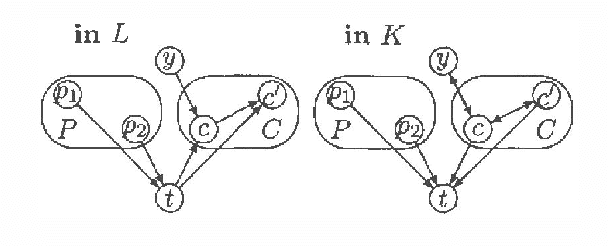
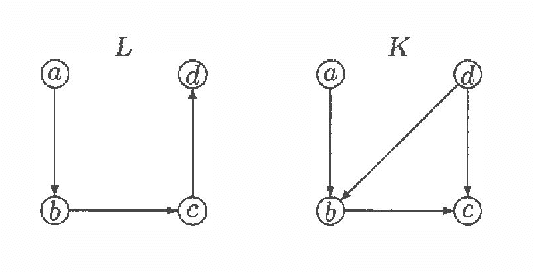
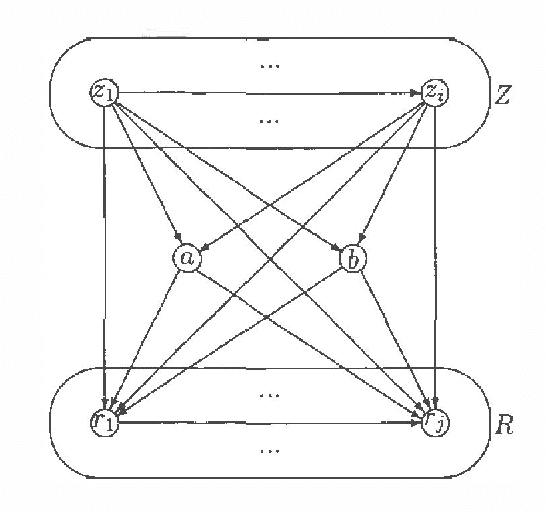
Every directed acyclic graph (DAG) over a finite non-empty set of variables (= nodes) N induces an independence model over N, which is a list of conditional independence statements over N.The inclusion problem is how to characterize (in graphical terms) whether all independence statements in the model induced by a DAG K are in the model induced by a second DAG L. Meek (1997) conjectured that this inclusion holds iff there exists a sequence of DAGs from L to K such that only certain 'legal' arrow reversal and 'legal' arrow adding operations are performed to get the next DAG in the sequence.In this paper we give several characterizations of inclusion of DAG models and verify Meek's conjecture in the case that the DAGs K and L differ in at most one adjacency. As a warming up a rigorous proof of well-known graphical characterizations of equivalence of DAGs, which is a highly related problem, is given.

Dimension Correction for Hierarchical Latent Class Models

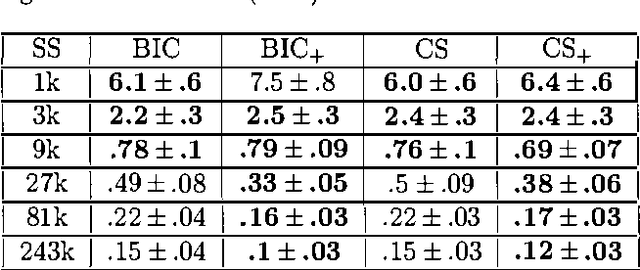
Model complexity is an important factor to consider when selecting among graphical models. When all variables are observed, the complexity of a model can be measured by its standard dimension, i.e. the number of independent parameters. When hidden variables are present, however, standard dimension might no longer be appropriate. One should instead use effective dimension (Geiger et al. 1996). This paper is concerned with the computation of effective dimension. First we present an upper bound on the effective dimension of a latent class (LC) model. This bound is tight and its computation is easy. We then consider a generalization of LC models called hierarchical latent class (HLC) models (Zhang 2002). We show that the effective dimension of an HLC model can be obtained from the effective dimensions of some related LC models. We also demonstrate empirically that using effective dimension in place of standard dimension improves the quality of models learned from data.

On Local Optima in Learning Bayesian Networks

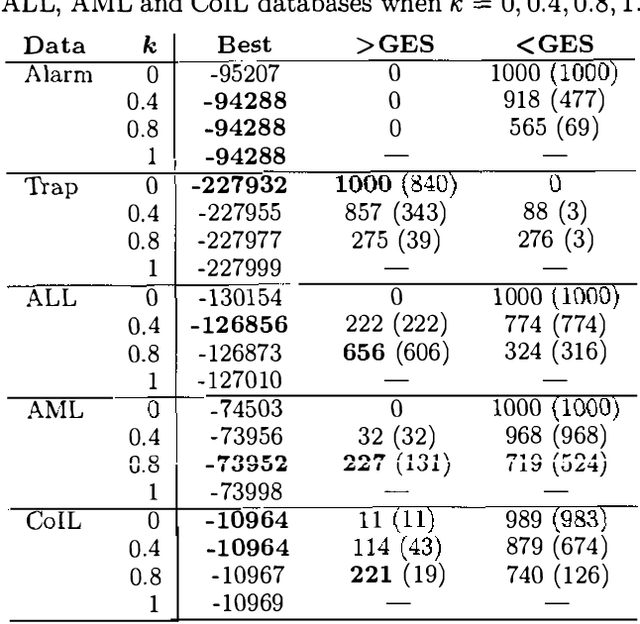
This paper proposes and evaluates the k-greedy equivalence search algorithm (KES) for learning Bayesian networks (BNs) from complete data. The main characteristic of KES is that it allows a trade-off between greediness and randomness, thus exploring different good local optima. When greediness is set at maximum, KES corresponds to the greedy equivalence search algorithm (GES). When greediness is kept at minimum, we prove that under mild assumptions KES asymptotically returns any inclusion optimal BN with nonzero probability. Experimental results for both synthetic and real data are reported showing that KES often finds a better local optima than GES. Moreover, we use KES to experimentally confirm that the number of different local optima is often huge.