On characterizing Inclusion of Bayesian Networks
Paper and Code
Jan 10, 2013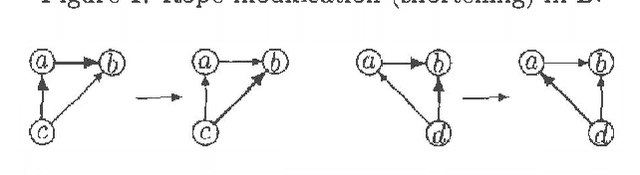
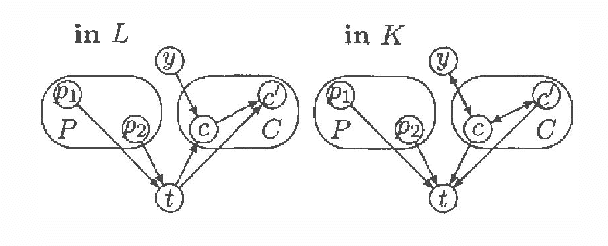
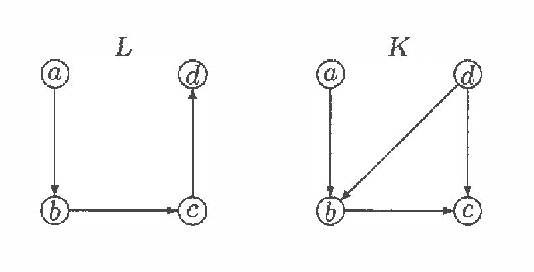
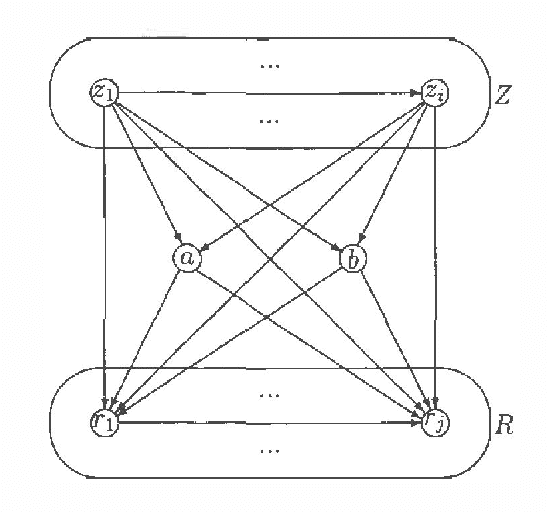
Every directed acyclic graph (DAG) over a finite non-empty set of variables (= nodes) N induces an independence model over N, which is a list of conditional independence statements over N.The inclusion problem is how to characterize (in graphical terms) whether all independence statements in the model induced by a DAG K are in the model induced by a second DAG L. Meek (1997) conjectured that this inclusion holds iff there exists a sequence of DAGs from L to K such that only certain 'legal' arrow reversal and 'legal' arrow adding operations are performed to get the next DAG in the sequence.In this paper we give several characterizations of inclusion of DAG models and verify Meek's conjecture in the case that the DAGs K and L differ in at most one adjacency. As a warming up a rigorous proof of well-known graphical characterizations of equivalence of DAGs, which is a highly related problem, is given.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge