Optimizing Causal Orderings for Generating DAGs from Data

An algorithm for generating the structure of a directed acyclic graph from data using the notion of causal input lists is presented. The algorithm manipulates the ordering of the variables with operations which very much resemble arc reversal. Operations are only applied if the DAG after the operation represents at least the independencies represented by the DAG before the operation until no more arcs can be removed from the DAG. The resulting DAG is a minimal l-map.

A Stratified Simulation Scheme for Inference in Bayesian Belief Networks

Simulation schemes for probabilistic inference in Bayesian belief networks offer many advantages over exact algorithms; for example, these schemes have a linear and thus predictable runtime while exact algorithms have exponential runtime. Experiments have shown that likelihood weighting is one of the most promising simulation schemes. In this paper, we present a new simulation scheme that generates samples more evenly spread in the sample space than the likelihood weighting scheme. We show both theoretically and experimentally that the stratified scheme outperforms likelihood weighting in average runtime and error in estimates of beliefs.

Properties of Bayesian Belief Network Learning Algorithms

Bayesian belief network learning algorithms have three basic components: a measure of a network structure and a database, a search heuristic that chooses network structures to be considered, and a method of estimating the probability tables from the database. This paper contributes to all these three topics. The behavior of the Bayesian measure of Cooper and Herskovits and a minimum description length (MDL) measure are compared with respect to their properties for both limiting size and finite size databases. It is shown that the MDL measure has more desirable properties than the Bayesian measure when a distribution is to be learned. It is shown that selecting belief networks with certain minimallity properties is NP-hard. This result justifies the use of search heuristics instead of exact algorithms for choosing network structures to be considered. In some cases, a collection of belief networks can be represented by a single belief network which leads to a new kind of probability table estimation called smoothing. We argue that smoothing can be efficiently implemented by incorporating it in the search heuristic. Experimental results suggest that for learning probabilities of belief networks smoothing is helpful.

Error Estimation in Approximate Bayesian Belief Network Inference

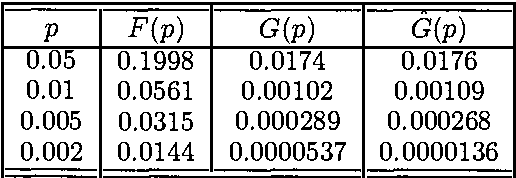
We can perform inference in Bayesian belief networks by enumerating instantiations with high probability thus approximating the marginals. In this paper, we present a method for determining the fraction of instantiations that has to be considered such that the absolute error in the marginals does not exceed a predefined value. The method is based on extreme value theory. Essentially, the proposed method uses the reversed generalized Pareto distribution to model probabilities of instantiations below a given threshold. Based on this distribution, an estimate of the maximal absolute error if instantiations with probability smaller than u are disregarded can be made.

On characterizing Inclusion of Bayesian Networks

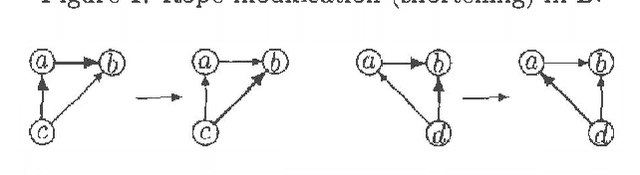
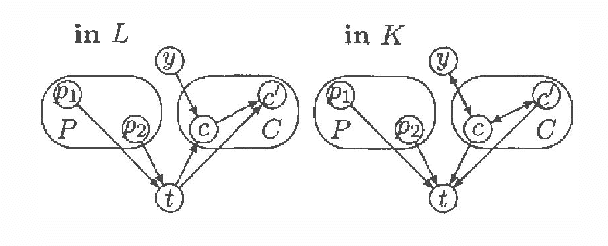
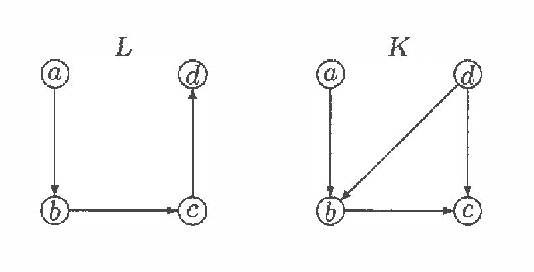
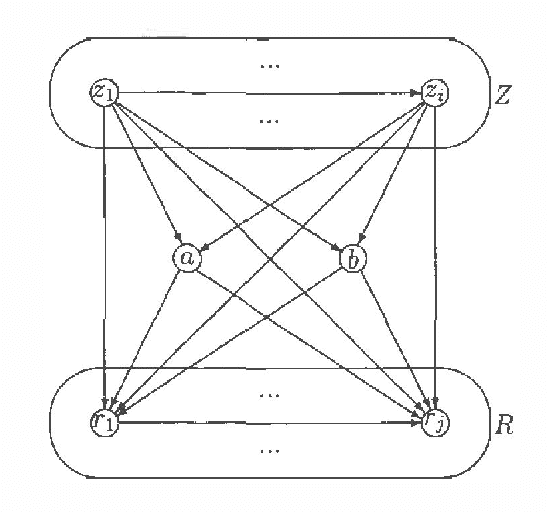
Every directed acyclic graph (DAG) over a finite non-empty set of variables (= nodes) N induces an independence model over N, which is a list of conditional independence statements over N.The inclusion problem is how to characterize (in graphical terms) whether all independence statements in the model induced by a DAG K are in the model induced by a second DAG L. Meek (1997) conjectured that this inclusion holds iff there exists a sequence of DAGs from L to K such that only certain 'legal' arrow reversal and 'legal' arrow adding operations are performed to get the next DAG in the sequence.In this paper we give several characterizations of inclusion of DAG models and verify Meek's conjecture in the case that the DAGs K and L differ in at most one adjacency. As a warming up a rigorous proof of well-known graphical characterizations of equivalence of DAGs, which is a highly related problem, is given.