Error Estimation in Approximate Bayesian Belief Network Inference

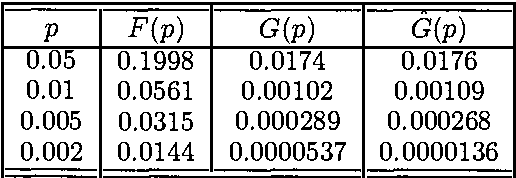
We can perform inference in Bayesian belief networks by enumerating instantiations with high probability thus approximating the marginals. In this paper, we present a method for determining the fraction of instantiations that has to be considered such that the absolute error in the marginals does not exceed a predefined value. The method is based on extreme value theory. Essentially, the proposed method uses the reversed generalized Pareto distribution to model probabilities of instantiations below a given threshold. Based on this distribution, an estimate of the maximal absolute error if instantiations with probability smaller than u are disregarded can be made.

Tail Sensitivity Analysis in Bayesian Networks

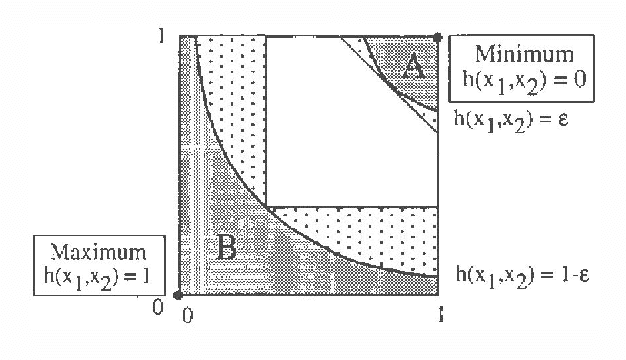
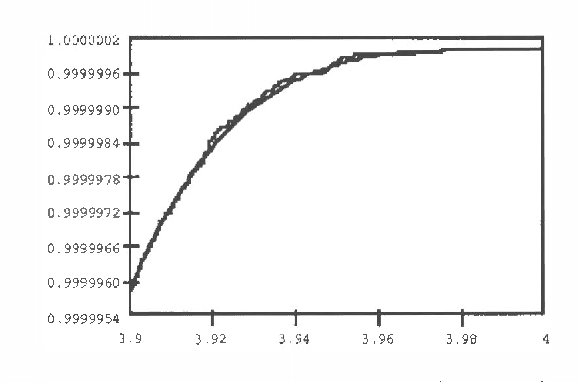
The paper presents an efficient method for simulating the tails of a target variable Z=h(X) which depends on a set of basic variables X=(X_1, ..., X_n). To this aim, variables X_i, i=1, ..., n are sequentially simulated in such a manner that Z=h(x_1, ..., x_i-1, X_i, ..., X_n) is guaranteed to be in the tail of Z. When this method is difficult to apply, an alternative method is proposed, which leads to a low rejection proportion of sample values, when compared with the Monte Carlo method. Both methods are shown to be very useful to perform a sensitivity analysis of Bayesian networks, when very large confidence intervals for the marginal/conditional probabilities are required, as in reliability or risk analysis. The methods are shown to behave best when all scores coincide. The required modifications for this to occur are discussed. The methods are illustrated with several examples and one example of application to a real case is used to illustrate the whole process.