Conditional independence structures over four discrete random variables revisited: conditional Ingleton inequalities

The paper deals with conditional linear information inequalities valid for entropy functions induced by discrete random variables. Specifically, the so-called conditional Ingleton inequalities are in the center of interest: these are valid under conditional independence assumptions on the inducing random variables. We discuss five inequalities of this particular type, four of which has appeared earlier in the literature. Besides the proof of the new fifth inequality, simpler proofs of (some of) former inequalities are presented. These five information inequalities are used to characterize all conditional independence structures induced by four discrete random variables.

Semigraphoids Are Two-Antecedental Approximations of Stochastic Conditional Independence Models

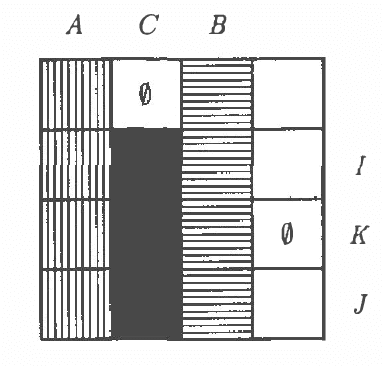
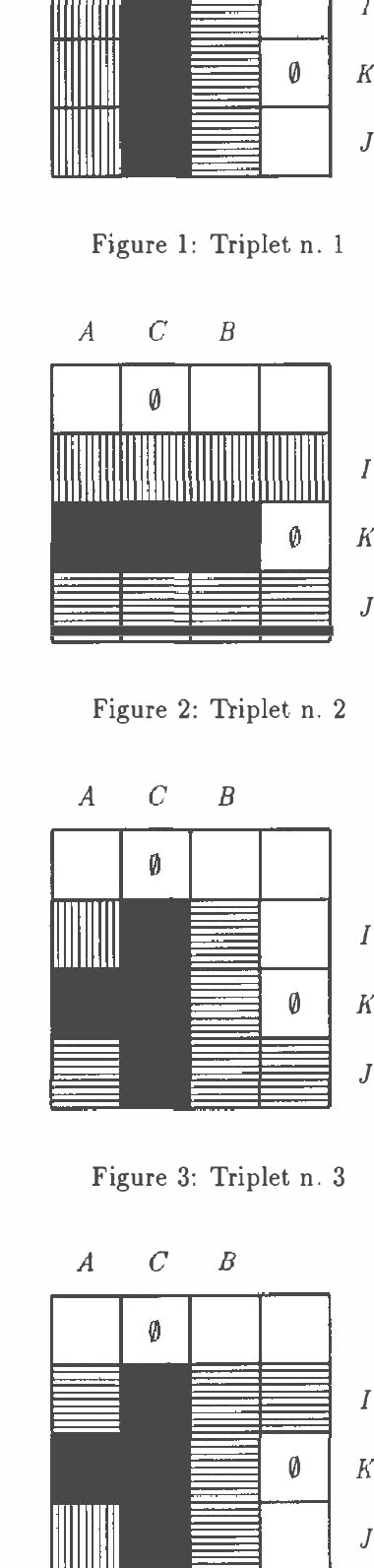
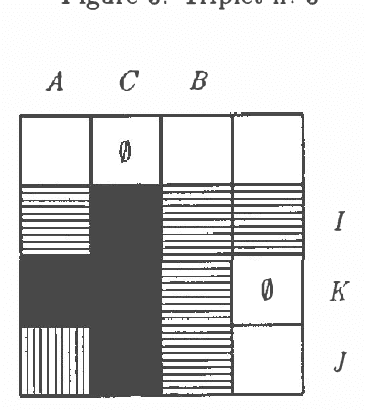
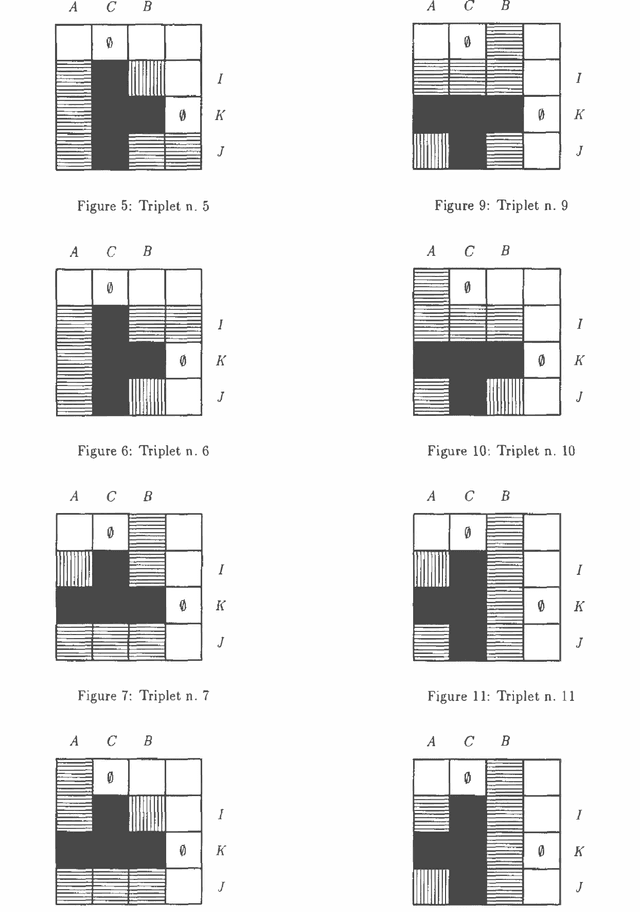
The semigraphoid closure of every couple of CI-statements (GI=conditional independence) is a stochastic CI-model. As a consequence of this result it is shown that every probabilistically sound inference rule for CI-model, having at most two antecedents, is derivable from the semigraphoid inference rules. This justifies the use of semigraphoids as approximations of stochastic CI-models in probabilistic reasoning. The list of all 19 potential dominant elements of the mentioned semigraphoid closure is given as a byproduct.

On Separation Criterion and Recovery Algorithm for Chain Graphs

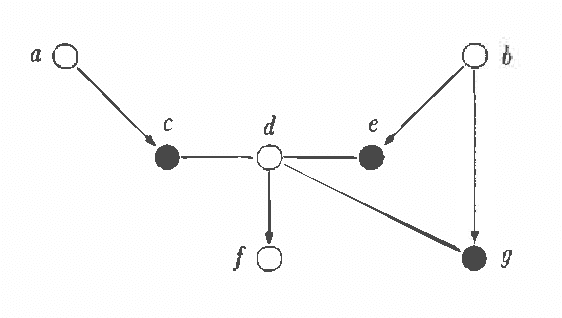
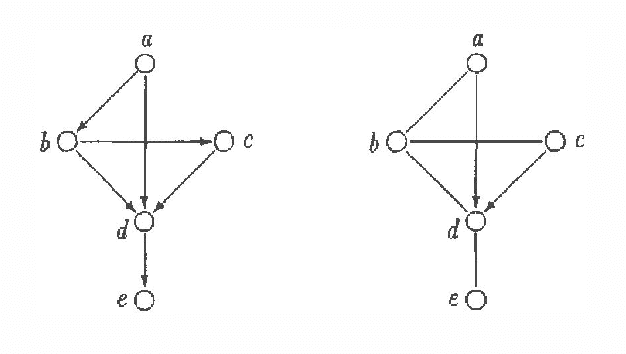
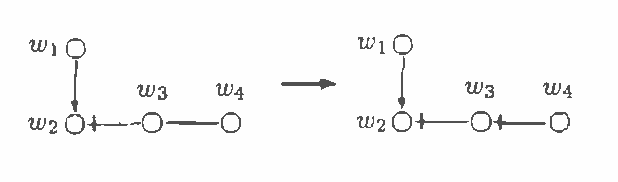
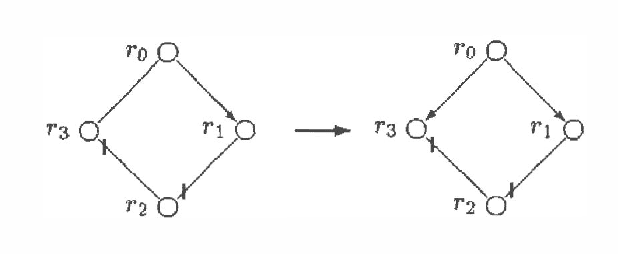
Chain graphs give a natural unifying point of view on Markov and Bayesian networks and enlarge the potential of graphical models for description of conditional independence structures. In the paper a direct graphical separation criterion for chain graphs, called c-separation, which generalizes the d-separation criterion for Bayesian networks is introduced (recalled). It is equivalent to the classic moralization criterion for chain graphs and complete in sense that for every chain graph there exists a probability distribution satisfying exactly conditional independencies derivable from the chain graph by the c-separation criterion. Every class of Markov equivalent chain graphs can be uniquely described by a natural representative, called the largest chain graph. A recovery algorithm, which on basis of the (conditional) dependency model induced by an unknown chain graph finds the corresponding largest chain graph, is presented.

Bayesian Networks from the Point of View of Chain Graphs

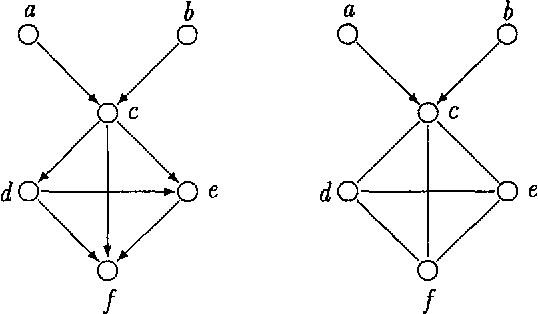
AThe paper gives a few arguments in favour of the use of chain graphs for description of probabilistic conditional independence structures. Every Bayesian network model can be equivalently introduced by means of a factorization formula with respect to a chain graph which is Markov equivalent to the Bayesian network. A graphical characterization of such graphs is given. The class of equivalent graphs can be represented by a distinguished graph which is called the largest chain graph. The factorization formula with respect to the largest chain graph is a basis of a proposal of how to represent the corresponding (discrete) probability distribution in a computer (i.e. parametrize it). This way does not depend on the choice of a particular Bayesian network from the class of equivalent networks and seems to be the most efficient way from the point of view of memory demands. A separation criterion for reading independency statements from a chain graph is formulated in a simpler way. It resembles the well-known d-separation criterion for Bayesian networks and can be implemented locally.

On characterizing Inclusion of Bayesian Networks

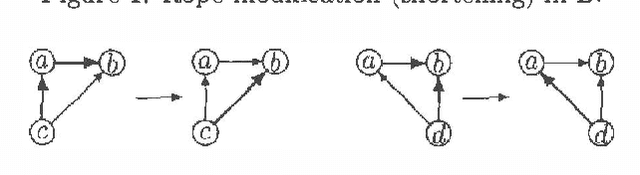
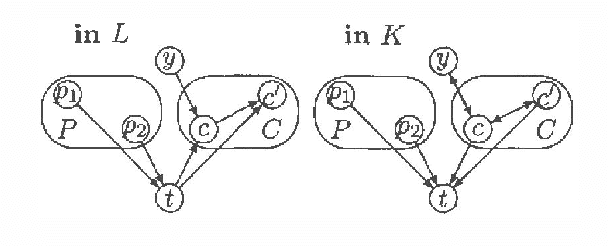
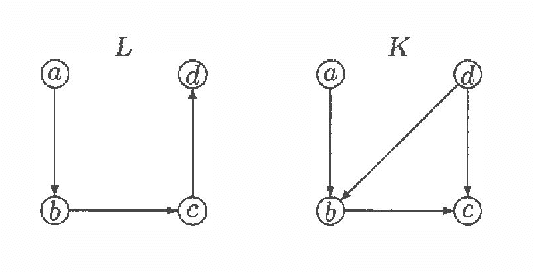
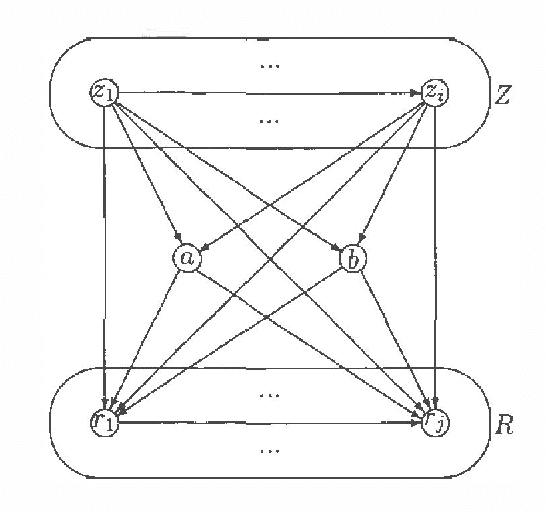
Every directed acyclic graph (DAG) over a finite non-empty set of variables (= nodes) N induces an independence model over N, which is a list of conditional independence statements over N.The inclusion problem is how to characterize (in graphical terms) whether all independence statements in the model induced by a DAG K are in the model induced by a second DAG L. Meek (1997) conjectured that this inclusion holds iff there exists a sequence of DAGs from L to K such that only certain 'legal' arrow reversal and 'legal' arrow adding operations are performed to get the next DAG in the sequence.In this paper we give several characterizations of inclusion of DAG models and verify Meek's conjecture in the case that the DAGs K and L differ in at most one adjacency. As a warming up a rigorous proof of well-known graphical characterizations of equivalence of DAGs, which is a highly related problem, is given.