On Separation Criterion and Recovery Algorithm for Chain Graphs
Paper and Code
Feb 13, 2013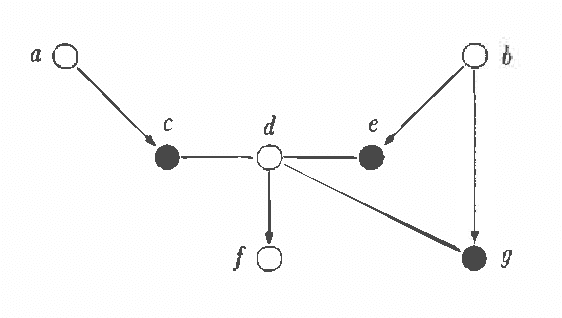
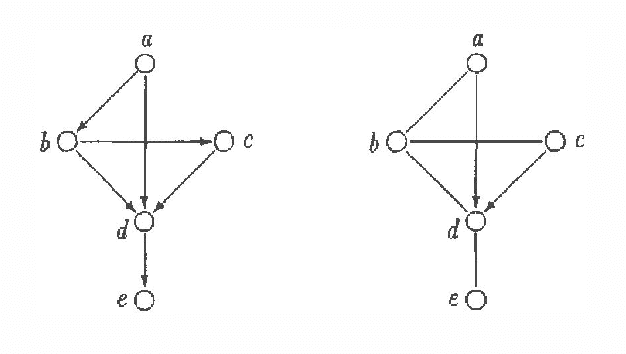
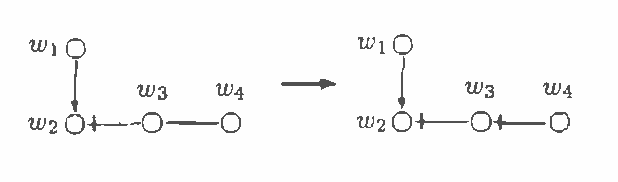
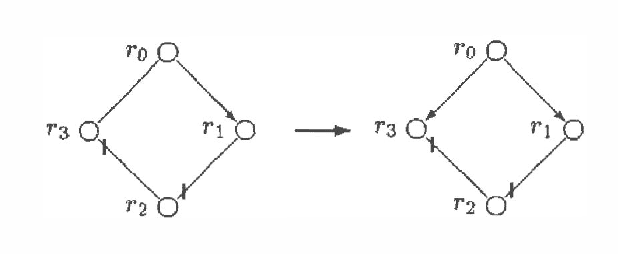
Chain graphs give a natural unifying point of view on Markov and Bayesian networks and enlarge the potential of graphical models for description of conditional independence structures. In the paper a direct graphical separation criterion for chain graphs, called c-separation, which generalizes the d-separation criterion for Bayesian networks is introduced (recalled). It is equivalent to the classic moralization criterion for chain graphs and complete in sense that for every chain graph there exists a probability distribution satisfying exactly conditional independencies derivable from the chain graph by the c-separation criterion. Every class of Markov equivalent chain graphs can be uniquely described by a natural representative, called the largest chain graph. A recovery algorithm, which on basis of the (conditional) dependency model induced by an unknown chain graph finds the corresponding largest chain graph, is presented.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge