Improved learning of Bayesian networks

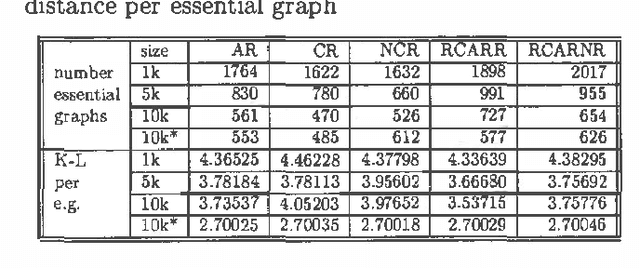
The search space of Bayesian Network structures is usually defined as Acyclic Directed Graphs (DAGs) and the search is done by local transformations of DAGs. But the space of Bayesian Networks is ordered by DAG Markov model inclusion and it is natural to consider that a good search policy should take this into account. First attempt to do this (Chickering 1996) was using equivalence classes of DAGs instead of DAGs itself. This approach produces better results but it is significantly slower. We present a compromise between these two approaches. It uses DAGs to search the space in such a way that the ordering by inclusion is taken into account. This is achieved by repetitive usage of local moves within the equivalence class of DAGs. We show that this new approach produces better results than the original DAGs approach without substantial change in time complexity. We present empirical results, within the framework of heuristic search and Markov Chain Monte Carlo, provided through the Alarm dataset.