Jens D. Nielsen
On Local Optima in Learning Bayesian Networks
Oct 19, 2012
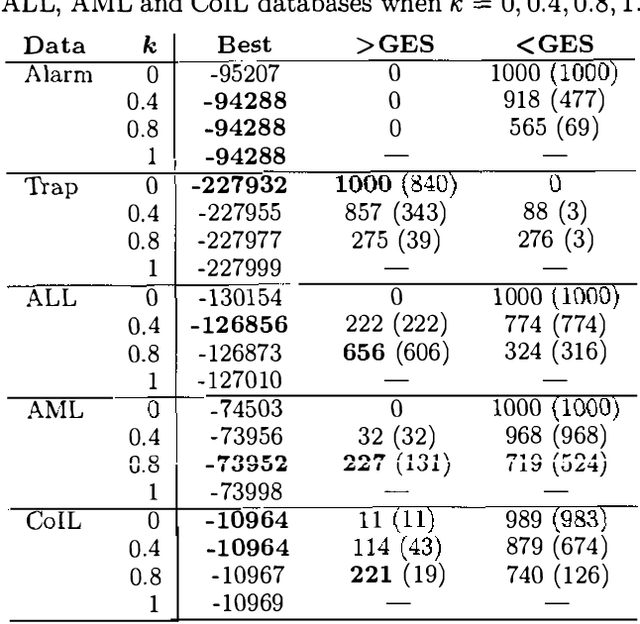
Abstract:This paper proposes and evaluates the k-greedy equivalence search algorithm (KES) for learning Bayesian networks (BNs) from complete data. The main characteristic of KES is that it allows a trade-off between greediness and randomness, thus exploring different good local optima. When greediness is set at maximum, KES corresponds to the greedy equivalence search algorithm (GES). When greediness is kept at minimum, we prove that under mild assumptions KES asymptotically returns any inclusion optimal BN with nonzero probability. Experimental results for both synthetic and real data are reported showing that KES often finds a better local optima than GES. Moreover, we use KES to experimentally confirm that the number of different local optima is often huge.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge