Dimension Correction for Hierarchical Latent Class Models
Paper and Code
Dec 12, 2012


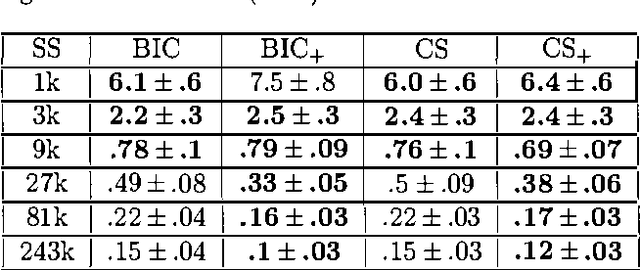
Model complexity is an important factor to consider when selecting among graphical models. When all variables are observed, the complexity of a model can be measured by its standard dimension, i.e. the number of independent parameters. When hidden variables are present, however, standard dimension might no longer be appropriate. One should instead use effective dimension (Geiger et al. 1996). This paper is concerned with the computation of effective dimension. First we present an upper bound on the effective dimension of a latent class (LC) model. This bound is tight and its computation is easy. We then consider a generalization of LC models called hierarchical latent class (HLC) models (Zhang 2002). We show that the effective dimension of an HLC model can be obtained from the effective dimensions of some related LC models. We also demonstrate empirically that using effective dimension in place of standard dimension improves the quality of models learned from data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge