Jennifer Barry
NovaFlow: Zero-Shot Manipulation via Actionable Flow from Generated Videos
Oct 09, 2025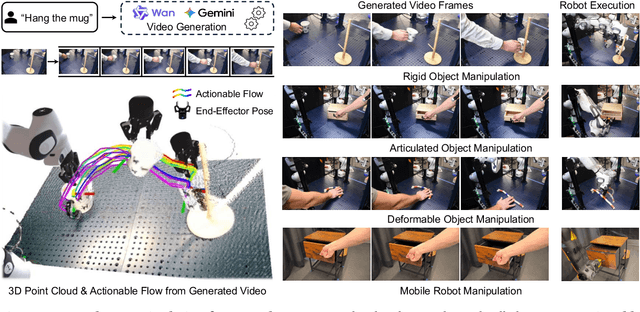
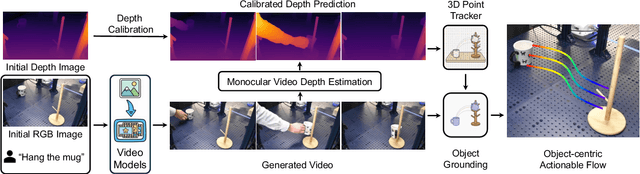


Abstract:Enabling robots to execute novel manipulation tasks zero-shot is a central goal in robotics. Most existing methods assume in-distribution tasks or rely on fine-tuning with embodiment-matched data, limiting transfer across platforms. We present NovaFlow, an autonomous manipulation framework that converts a task description into an actionable plan for a target robot without any demonstrations. Given a task description, NovaFlow synthesizes a video using a video generation model and distills it into 3D actionable object flow using off-the-shelf perception modules. From the object flow, it computes relative poses for rigid objects and realizes them as robot actions via grasp proposals and trajectory optimization. For deformable objects, this flow serves as a tracking objective for model-based planning with a particle-based dynamics model. By decoupling task understanding from low-level control, NovaFlow naturally transfers across embodiments. We validate on rigid, articulated, and deformable object manipulation tasks using a table-top Franka arm and a Spot quadrupedal mobile robot, and achieve effective zero-shot execution without demonstrations or embodiment-specific training. Project website: https://novaflow.lhy.xyz/.
Practice Makes Perfect: Planning to Learn Skill Parameter Policies
Feb 22, 2024Abstract:One promising approach towards effective robot decision making in complex, long-horizon tasks is to sequence together parameterized skills. We consider a setting where a robot is initially equipped with (1) a library of parameterized skills, (2) an AI planner for sequencing together the skills given a goal, and (3) a very general prior distribution for selecting skill parameters. Once deployed, the robot should rapidly and autonomously learn to improve its performance by specializing its skill parameter selection policy to the particular objects, goals, and constraints in its environment. In this work, we focus on the active learning problem of choosing which skills to practice to maximize expected future task success. We propose that the robot should estimate the competence of each skill, extrapolate the competence (asking: "how much would the competence improve through practice?"), and situate the skill in the task distribution through competence-aware planning. This approach is implemented within a fully autonomous system where the robot repeatedly plans, practices, and learns without any environment resets. Through experiments in simulation, we find that our approach learns effective parameter policies more sample-efficiently than several baselines. Experiments in the real-world demonstrate our approach's ability to handle noise from perception and control and improve the robot's ability to solve two long-horizon mobile-manipulation tasks after a few hours of autonomous practice.
Quantum POMDPs
Oct 01, 2014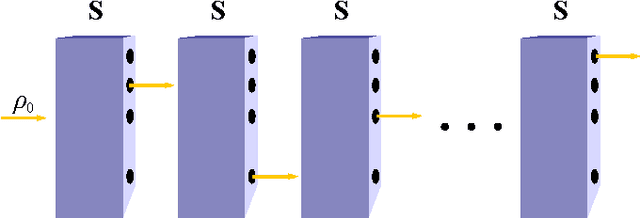
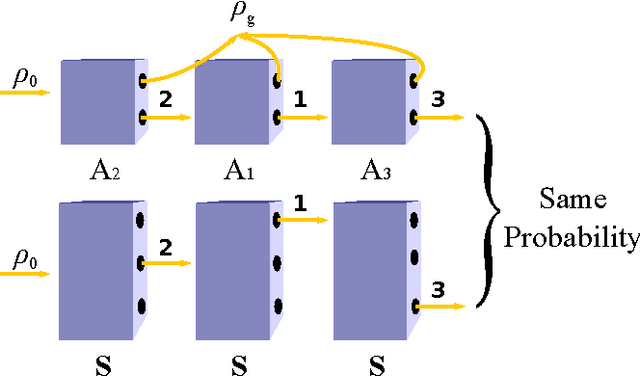
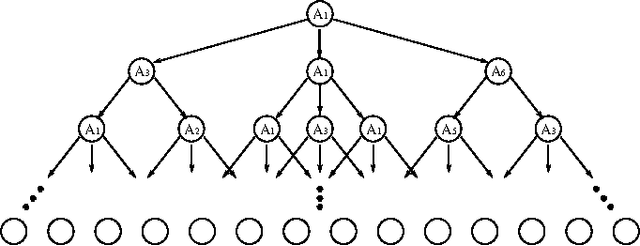
Abstract:We present quantum observable Markov decision processes (QOMDPs), the quantum analogues of partially observable Markov decision processes (POMDPs). In a QOMDP, an agent's state is represented as a quantum state and the agent can choose a superoperator to apply. This is similar to the POMDP belief state, which is a probability distribution over world states and evolves via a stochastic matrix. We show that the existence of a policy of at least a certain value has the same complexity for QOMDPs and POMDPs in the polynomial and infinite horizon cases. However, we also prove that the existence of a policy that can reach a goal state is decidable for goal POMDPs and undecidable for goal QOMDPs.
* 13 pages, 3 figures, revised version (fixes several errors, discusses related work)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge