Training-Free Exponential Extension of Sliding Window Context with Cascading KV Cache

The context window within a transformer provides a form of active memory for the current task, which can be useful for few-shot learning and conditional generation, both which depend heavily on previous context tokens. However, as the context length grows, the computational cost increases quadratically. Recent works have shown that saving a few initial tokens along with a fixed-sized sliding window leads to stable streaming generation with linear complexity in transformer-based Large Language Models (LLMs). However, they make suboptimal use of the fixed window by naively evicting all tokens unconditionally from the key-value (KV) cache once they reach the end of the window, resulting in tokens being forgotten and no longer able to affect subsequent predictions. To overcome this limitation, we propose a novel mechanism for storing longer sliding window contexts with the same total cache size by keeping separate cascading sub-cache buffers whereby each subsequent buffer conditionally accepts a fraction of the relatively more important tokens evicted from the previous buffer. Our method results in a dynamic KV cache that can store tokens from the more distant past than a fixed, static sliding window approach. Our experiments show improvements of 5.6% on long context generation (LongBench), 1.2% in streaming perplexity (PG19), and 0.6% in language understanding (MMLU STEM) using LLMs given the same fixed cache size. Additionally, we provide an efficient implementation that improves the KV cache latency from 1.33ms per caching operation to 0.54ms, a 59% speedup over previous work.

SEA: Sparse Linear Attention with Estimated Attention Mask

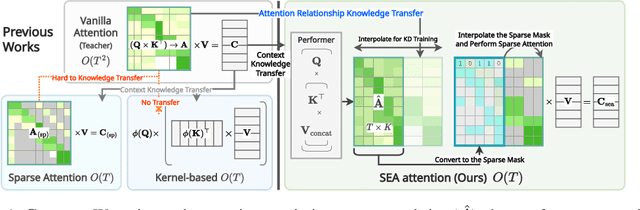
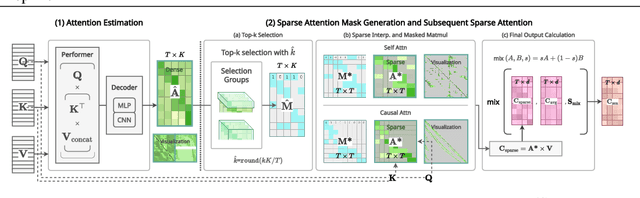
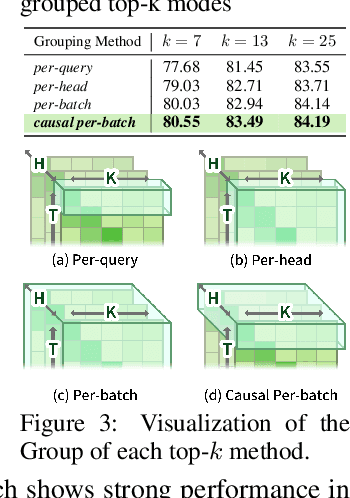
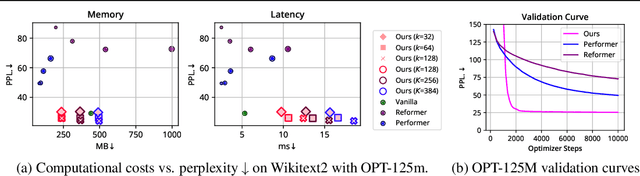
The transformer architecture has made breakthroughs in recent years on tasks which require modeling pairwise relationships between sequential elements, as is the case in natural language understanding. However, transformers struggle with long sequences due to the quadratic complexity of the attention operation, and previous research has aimed to lower the complexity by sparsifying or linearly approximating the attention matrix. Yet, these approaches cannot straightforwardly distill knowledge from a teacher's attention matrix, and often require complete retraining from scratch. Furthermore, previous sparse and linear approaches may also lose interpretability if they do not produce full quadratic attention matrices. To address these challenges, we propose SEA: Sparse linear attention with an Estimated Attention mask. SEA estimates the attention matrix with linear complexity via kernel-based linear attention, then creates a sparse approximation to the full attention matrix with a top-k selection to perform a sparse attention operation. For language modeling tasks (Wikitext2), previous linear and sparse attention methods show a roughly two-fold worse perplexity scores over the quadratic OPT-125M baseline, while SEA achieves an even better perplexity than OPT-125M, using roughly half as much memory as OPT-125M. Moreover, SEA maintains an interpretable attention matrix and can utilize knowledge distillation to lower the complexity of existing pretrained transformers. We believe that our work will have a large practical impact, as it opens the possibility of running large transformers on resource-limited devices with less memory.

Exploring The Role of Mean Teachers in Self-supervised Masked Auto-Encoders

Masked image modeling (MIM) has become a popular strategy for self-supervised learning~(SSL) of visual representations with Vision Transformers. A representative MIM model, the masked auto-encoder (MAE), randomly masks a subset of image patches and reconstructs the masked patches given the unmasked patches. Concurrently, many recent works in self-supervised learning utilize the student/teacher paradigm which provides the student with an additional target based on the output of a teacher composed of an exponential moving average (EMA) of previous students. Although common, relatively little is known about the dynamics of the interaction between the student and teacher. Through analysis on a simple linear model, we find that the teacher conditionally removes previous gradient directions based on feature similarities which effectively acts as a conditional momentum regularizer. From this analysis, we present a simple SSL method, the Reconstruction-Consistent Masked Auto-Encoder (RC-MAE) by adding an EMA teacher to MAE. We find that RC-MAE converges faster and requires less memory usage than state-of-the-art self-distillation methods during pre-training, which may provide a way to enhance the practicality of prohibitively expensive self-supervised learning of Vision Transformer models. Additionally, we show that RC-MAE achieves more robustness and better performance compared to MAE on downstream tasks such as ImageNet-1K classification, object detection, and instance segmentation.

Universal Mini-Batch Consistency for Set Encoding Functions

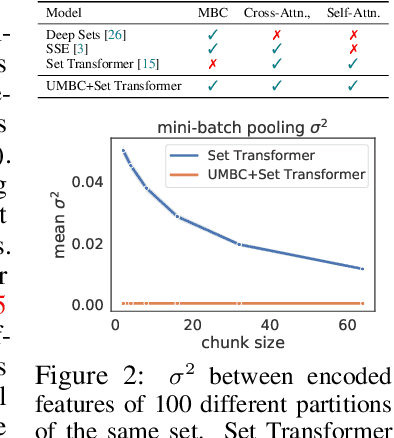
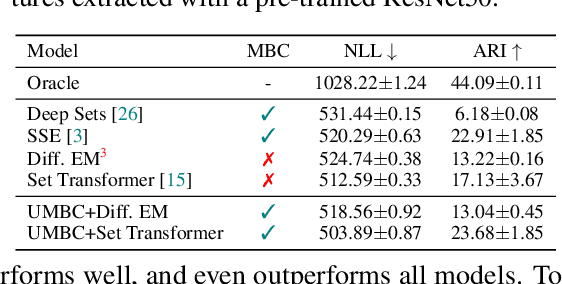
Previous works have established solid foundations for neural set functions, as well as effective architectures which preserve the necessary properties for operating on sets, such as being invariant to permutations of the set elements. Subsequently, Mini-Batch Consistency (MBC), the ability to sequentially process any permutation of any random set partition scheme while maintaining consistency guarantees on the output, has been established but with limited options for network architectures. We further study the MBC property in neural set encoding functions, establishing a method for converting arbitrary non-MBC models to satisfy MBC. In doing so, we provide a framework for a universally-MBC (UMBC) class of set functions. Additionally, we explore an interesting dropout strategy made possible by our framework, and investigate its effects on probabilistic calibration under test-time distributional shifts. We validate UMBC with proofs backed by unit tests, also providing qualitative/quantitative experiments on toy data, clean and corrupted point cloud classification, and amortized clustering on ImageNet. The results demonstrate the utility of UMBC, and we further discover that our dropout strategy improves uncertainty calibration.

Mini-Batch Consistent Slot Set Encoder for Scalable Set Encoding

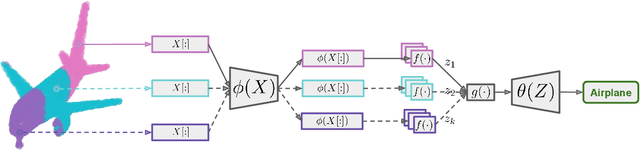
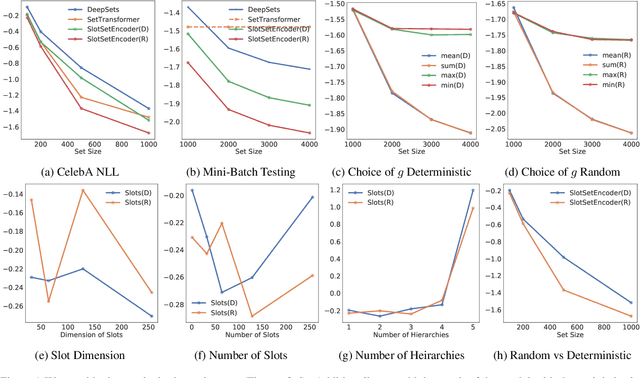
Most existing set encoding algorithms operate under the assumption that all the elements of the set are accessible during training and inference. Additionally, it is assumed that there are enough computational resources available for concurrently processing sets of large cardinality. However, both assumptions fail when the cardinality of the set is prohibitively large such that we cannot even load the set into memory. In more extreme cases, the set size could be potentially unlimited, and the elements of the set could be given in a streaming manner, where the model receives subsets of the full set data at irregular intervals. To tackle such practical challenges in large-scale set encoding, we go beyond the usual constraints of invariance and equivariance and introduce a new property termed Mini-Batch Consistency that is required for large scale mini-batch set encoding. We present a scalable and efficient set encoding mechanism that is amenable to mini-batch processing with respect to set elements and capable of updating set representations as more data arrives. The proposed method respects the required symmetries of invariance and equivariance as well as being Mini-Batch Consistent for random partitions of the input set. We perform extensive experiments and show that our method is computationally efficient and results in rich set encoding representations for set-structured data.

Improving Uncertainty Calibration via Prior Augmented Data

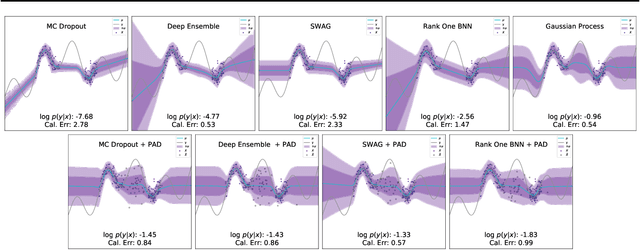
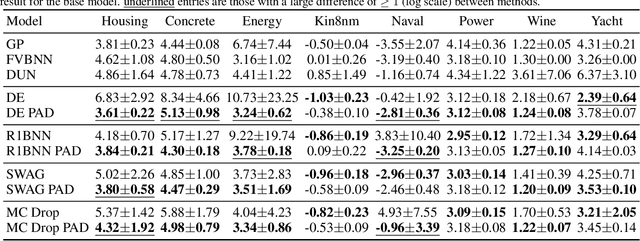
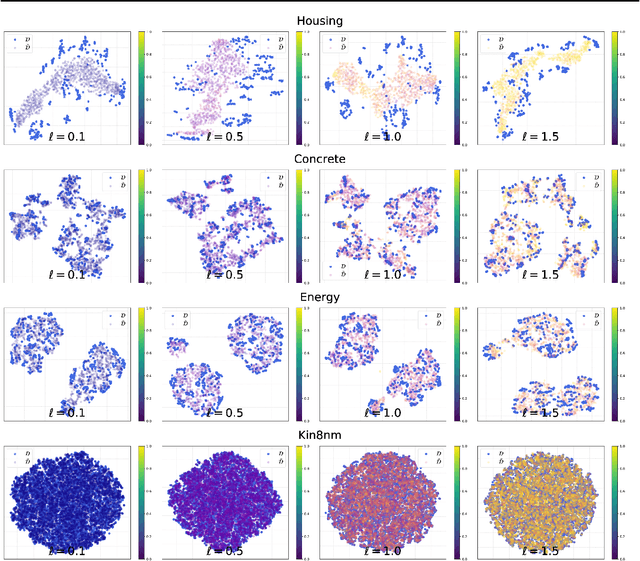
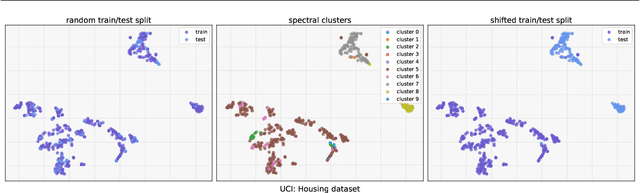
Neural networks have proven successful at learning from complex data distributions by acting as universal function approximators. However, they are often overconfident in their predictions, which leads to inaccurate and miscalibrated probabilistic predictions. The problem of overconfidence becomes especially apparent in cases where the test-time data distribution differs from that which was seen during training. We propose a solution to this problem by seeking out regions of feature space where the model is unjustifiably overconfident, and conditionally raising the entropy of those predictions towards that of the prior distribution of the labels. Our method results in a better calibrated network and is agnostic to the underlying model structure, so it can be applied to any neural network which produces a probability density as an output. We demonstrate the effectiveness of our method and validate its performance on both classification and regression problems, applying it to recent probabilistic neural network models.