Improving Uncertainty Calibration via Prior Augmented Data
Paper and Code
Feb 22, 2021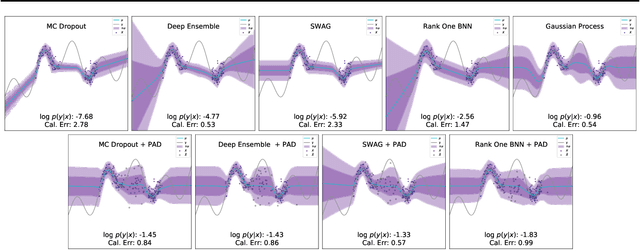
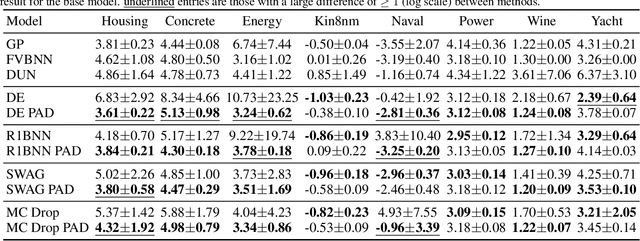

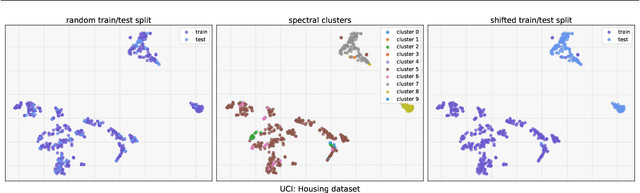
Neural networks have proven successful at learning from complex data distributions by acting as universal function approximators. However, they are often overconfident in their predictions, which leads to inaccurate and miscalibrated probabilistic predictions. The problem of overconfidence becomes especially apparent in cases where the test-time data distribution differs from that which was seen during training. We propose a solution to this problem by seeking out regions of feature space where the model is unjustifiably overconfident, and conditionally raising the entropy of those predictions towards that of the prior distribution of the labels. Our method results in a better calibrated network and is agnostic to the underlying model structure, so it can be applied to any neural network which produces a probability density as an output. We demonstrate the effectiveness of our method and validate its performance on both classification and regression problems, applying it to recent probabilistic neural network models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge