Andreis Bruno
Universal Mini-Batch Consistency for Set Encoding Functions
Aug 26, 2022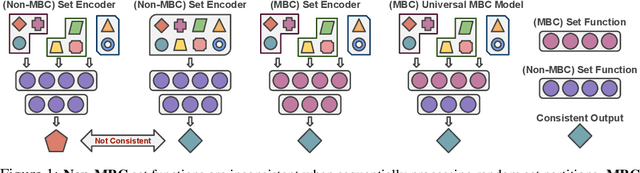

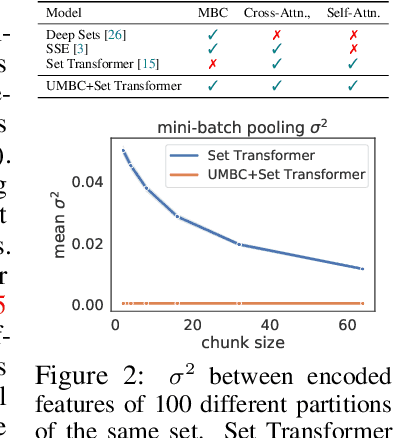
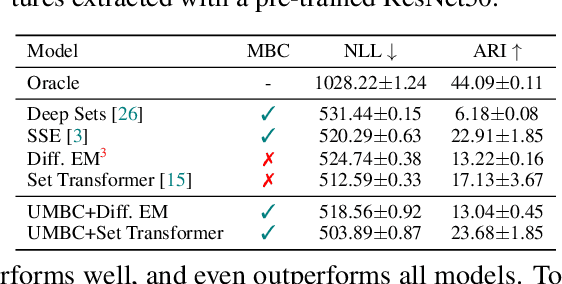
Abstract:Previous works have established solid foundations for neural set functions, as well as effective architectures which preserve the necessary properties for operating on sets, such as being invariant to permutations of the set elements. Subsequently, Mini-Batch Consistency (MBC), the ability to sequentially process any permutation of any random set partition scheme while maintaining consistency guarantees on the output, has been established but with limited options for network architectures. We further study the MBC property in neural set encoding functions, establishing a method for converting arbitrary non-MBC models to satisfy MBC. In doing so, we provide a framework for a universally-MBC (UMBC) class of set functions. Additionally, we explore an interesting dropout strategy made possible by our framework, and investigate its effects on probabilistic calibration under test-time distributional shifts. We validate UMBC with proofs backed by unit tests, also providing qualitative/quantitative experiments on toy data, clean and corrupted point cloud classification, and amortized clustering on ImageNet. The results demonstrate the utility of UMBC, and we further discover that our dropout strategy improves uncertainty calibration.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge